(Solved): Water flows steadily through the variable area horizontal pipe shown in the figure below. The cente ...

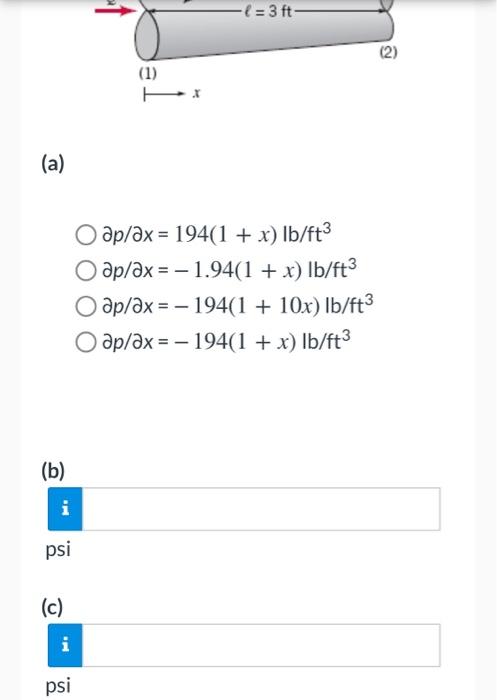
Water flows steadily through the variable area horizontal pipe shown in the figure below. The centerline velocity is given by \( \mathbf{V}=10(1+x) \hat{i} \mathrm{ft} / \mathrm{s} \), where \( x \) is in feet. Viscous effects are neglected. (a) Determine the pressure gradient, \( \partial p / \partial x \) (as a function of \( x \) ), needed to produce this flow. If the pressure at section (1) is \( 105 \mathrm{psi} \), determine the pressure at (2) by \( (b) \) integration of the pressure gradient obtained in (a) and (c) application of the Bernoulli equation. \( \partial p / \partial x=194(1+x) \mathrm{lb} / \mathrm{ft}^{3} \) \( \partial p / \partial x=-1.94(1+x) \mathrm{lb} / \mathrm{ft}^{3} \) \( \partial p / \partial x=-194(1+10 x) \mathrm{lb} / \mathrm{ft}^{3} \) \( \partial p / \partial x=-194(1+x) \mathrm{lb} / \mathrm{ft}^{3} \)