(Solved): Verify the identity. \[ \cos ^{3} x-\sin ^{3} x=(\cos x-\sin x)(1+\cos x \sin x) \] Choose the sequ ...

Verify the identity. \[ \cos ^{3} x-\sin ^{3} x=(\cos x-\sin x)(1+\cos x \sin x) \] Choose the sequence of steps below that verifies the identity. A. \( \cos ^{3} x-\sin ^{3} x=(\cos x-\sin x)\left(\cos ^{2} x+\cos x \sin x+\sin ^{2} x\right) \) \( =(\cos x-\sin x)(1+\cos x \sin x) \) B. \( \cos ^{3} x-\sin ^{3} x=(\cos x+\sin x)\left(\cos ^{2} x-\cos x \sin x+\sin ^{2} x\right) \) \( =(\cos x-\sin x)(1+\cos x \sin x) \) C. \( \cos ^{3} x-\sin ^{3} x=(\cos x+\sin x)\left(\cos ^{2} x-2 \cos x \sin x+\sin ^{2} x\right) \) \( =(\cos x-\sin x)(1+\cos x \sin x) \) D. 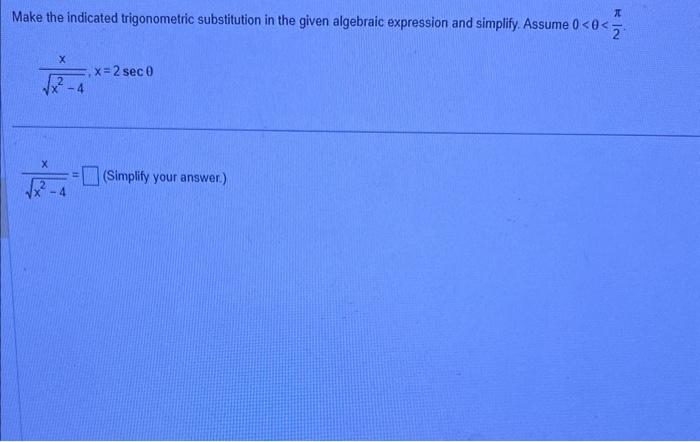\( \cos ^{3} x-\sin ^{3} x=(\cos x-\sin x)\left(\cos ^{2} x+2 \cos x \sin x+\sin ^{2} x\right) \) \( =(\cos x-\sin x)(1+\cos x \sin x) \) Make the indicated trigonometric substitution in the given algebraic expression and simplify. Assume \( 0<\theta<\frac{\pi}{2} \). \( \frac{x}{\sqrt{x^{2}-4}}, x=2 \sec \theta \) \( \frac{x}{\sqrt{x^{2}-4}}=\quad \) (Simplify your answer.) Verify the identity. \[ \cos x \cot ^{2} x=\cos x \csc ^{2} x-\cos x \] Which of the following four statements establishes the identity? A. \( \cos x \cot ^{2} x=\frac{\sin ^{3} x}{\cos ^{2} x}=\frac{\sin x}{\cos ^{2} x}-\cos x=\cos x \csc ^{2} x-\cos x \) B. \( \cos x \cot ^{2} x=\frac{\cos ^{3} x}{\sin ^{2} x}=\frac{\sin x}{\cos ^{2} x}-\cos x=\cos x \csc ^{2} x-\cos x \) C. \( \cos x \cot ^{2} x=\frac{\cos ^{3} x}{\sin ^{2} x}=\frac{\cos x}{\sin ^{2} x}-\cos x=\cos x \csc ^{2} x-\cos x \) D. \( \cos x \cot ^{2} x=\frac{\sin ^{3} x}{\cos ^{2} x}=\frac{\cos x}{\sin ^{2} x}-\cos x=\cos x \csc ^{2} x-\cos x \) Establish the identity. \[ \csc u-\cot u=\frac{\sin u}{1+\cos u} \] Which of the following statements establishes the identity? A. \( \csc u-\cot u=\frac{1}{\sin u}-\frac{\cos u}{\sin u}=\left(\frac{1-\cos u}{\sin u}\right) \cdot\left(\frac{1+\cos u}{1+\cos u}\right)=\frac{1-\cos ^{2} u}{\sin u(1+\cos u)}=\frac{\sin ^{2} u}{\sin u(1+\cos u)}=\frac{\sin u}{1+\cos u} \) B. \( \csc u-\cot u=\frac{1}{\sin u}-\frac{\cos u}{\sin u}=\left(\frac{1-\cos u}{\sin u}\right) \cdot\left(\frac{1+\cos u}{1+\cos u}\right)=\frac{1+\cos ^{2} u}{\sin u(1+\cos u)}=\frac{\sin ^{2} u}{\sin u(1+\cos u)}=\frac{\sin u}{1+\cos u} \) C. \[ \csc u-\cot u=\frac{1}{\cos u}-\frac{\sin u}{\cos u}=\left(\frac{1-\sin u}{\cos u}\right) \cdot\left(\frac{1+\sin u}{1+\sin u}\right)=\frac{1+\sin ^{2} u}{\cos u(1+\sin u)}=\frac{\sin u}{1+\cos u} \] Establish the identity \( \frac{1-\sec \theta}{\tan \theta}-\frac{\tan \theta}{1-\sec \theta}=2 \cot \theta \) Which of the following shows the key steps in establishing the identity? A. \( \frac{1-\sec \theta}{\tan \theta}-\frac{\tan \theta}{1-\sec \theta}=\frac{(1+\sec \theta)^{2}-\tan ^{2} \theta}{\tan \theta(1+\sec \theta)}=\frac{2(1+\tan \theta)}{\sec \theta(1+\tan \theta)}=2 \cot \theta \) B. \( \frac{1-\sec \theta}{\tan \theta}-\frac{\tan \theta}{1-\sec \theta}=\frac{(1+\sec \theta)^{2}-\tan ^{2} \theta}{\tan \theta(1+\sec \theta)}=\frac{2}{\sec \theta}=2 \cot \theta \) C. \( \frac{1-\sec \theta}{\tan \theta}-\frac{\tan \theta}{1-\sec \theta}=\frac{(1-\sec \theta)^{2}-\tan ^{2} \theta}{\tan \theta(1-\sec \theta)}=\frac{2}{\sec \theta}=2 \cot \theta \) D. \( \frac{1-\sec \theta}{\tan \theta}-\frac{\tan \theta}{1-\sec \theta}=\frac{(1-\sec \theta)^{2}-\tan ^{2} \theta}{\tan \theta(1-\sec \theta)}=\frac{2(1-\sec \theta)}{\tan \theta(1-\sec \theta)}=2 \cot \theta \)