Home /
Expert Answers /
Algebra /
use-the-remainder-theorem-to-find-p-1-for-p-x-2-x-4-4-x-3-6-x-2-8-specificall-pa298
(Solved): Use the remainder theorem to find \( P(1) \) for \( P(x)=-2 x^{4}+4 x^{3}+6 x^{2}-8 \). Specificall ...
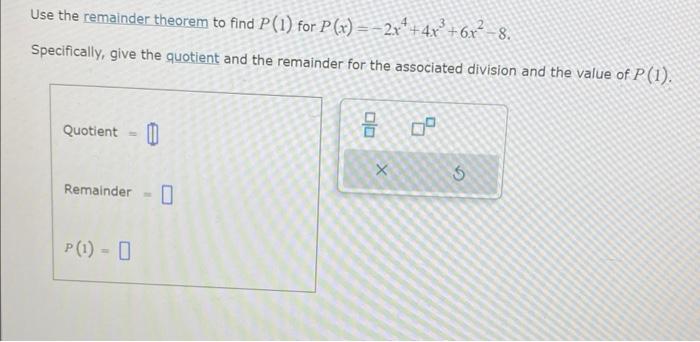
![For the polynomial below, 3 and 1 are zeros.
\[
f(x)=x^{4}-2 x^{3}-6 x^{2}+10 x-3
\]
Express \( f(x) \) as a product of linea](https://media.cheggcdn.com/study/02a/02a3b132-0ff8-410b-9403-52bc607014a9/image)
Use the remainder theorem to find \( P(1) \) for \( P(x)=-2 x^{4}+4 x^{3}+6 x^{2}-8 \). Specifically, give the quotient and the remainder for the associated division and the value of \( P(1) \).
For the polynomial below, 3 and 1 are zeros. \[ f(x)=x^{4}-2 x^{3}-6 x^{2}+10 x-3 \] Express \( f(x) \) as a product of linear factors.
Expert Answer
Given, polynomial function: P(x)=?2x4+4x3+6x2?8 According to remainder theorem when a polyn