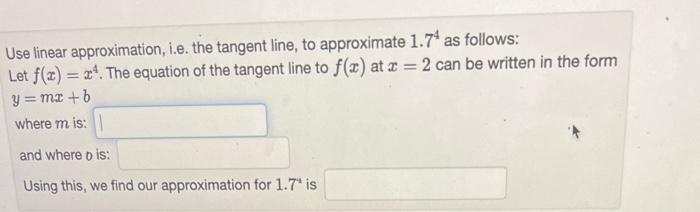
(Solved): Use linear approximation, i.e. the tangent line, to approximate \( 1.7^{4} \) as follows: Let \( f( ...

Use linear approximation, i.e. the tangent line, to approximate \( 1.7^{4} \) as follows: Let \( f(x)=x^{4} \). The equation of the tangent line to \( f(x) \) at \( x=2 \) can be written in the form \( y=m x+b \) where \( m \) is: and where \( \mathrm{o} \) is: Using this, we find our approximation for \( 1.7^{4} \) is Use linear approximation to approximate \( \sqrt{25.2} \) as follows. Let \( f(x)=\sqrt{x} \). The equation of the tangent line to \( f(x) \) at \( x=25 \) can be written in form \( y=m x+b \). Compute \( m \) and \( b \). \[ \begin{array}{l} m= \\ b= \end{array} \] Using this find the approximation for \( \sqrt{25.2} \). Answer: Find the linear approximation of \( f(x)=\ln x \) at \( x=1 \) and use it to estimate \( \ln (1.36) \). \[ L(x)= \] \( \ln 1.36 \approx \) Use linear approximation, i.e. the tangent line, to approximate \( \frac{1}{0.504} \) as follows: Let \( f(x)=\frac{1}{x} \) and find the equation of the tangent line to \( f(x) \) at a "nice" point near \( (0.504, f(0.504)) \). Then use this to approximate \( \frac{1}{0.504} \).