(Solved): Use 2.026 as the weight of iolab device just do LS! #1 and 2 and find the maximum tension force L ...

Use 2.026 as the weight of iolab device just do LS! #1 and 2 and find the maximum tension force

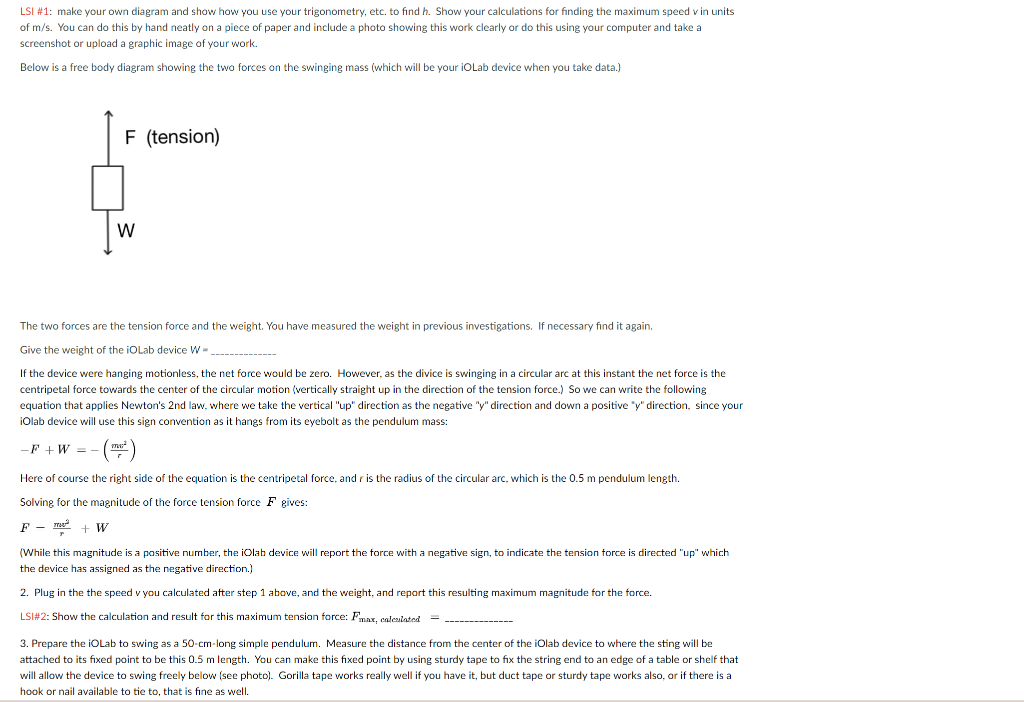
LSI \#1: make your own diagram and show how you use your trigonometry, etc. to find \( h \). Show your calculations for finding the maximum speed \( v \) in units of \( \mathrm{m} / \mathrm{s} \). You can do this by hand neatly on a piece of paper and include a photo showing this work clearly or do this using your computer and take a screenshot or upload a graphic image of your work. Below is a free body diagram showing the two forces on the swinging mass (which will be your iOLab device when you take data.) The two forces are the tension force and the weight. You have measured the weight in previous investigations. If necessary find it again. Give the weight of the iOLab device \( W= \) If the device were hanging motionless, the net force would be zero. However, as the divice is swinging in a circular arc at this instant the net force is the centripetal force towards the center of the circular motion (vertically straight up in the direction of the tension force.) So we can write the following equation that applies Newton's 2 nd law, where we take the vertical "up" direction as the negative " \( y \) " direction and down a positive " \( y \) " direction, since your iOlab device will use this sign convention as it hangs from its eyebolt as the pendulum mass: \[ -F+W=-\left(\frac{m v^{2}}{r}\right) \] Here of course the right side of the equation is the centripetal force, and \( r \) is the radius of the circular arc, which is the \( 0.5 \mathrm{~m} \) pendulum length. Solving for the magnitude of the force tension force \( F \) gives: \[ F-\frac{m e^{2}}{r}+W \] (While this magnitude is a positive number, the iOlab device will report the force with a negative sign, to indicate the tension torce is directed "up" which the device has assigned as the negative direction.) 2. Plug in the the speed \( v \) you calculated after step 1 above, and the weight, and report this resulting maximum magnitude for the force. LSI\#2: Show the calculation and result for this maximum tension force: \( F_{\max } \), calculnted \( = \) 3. Prepare the iOLab to swing as a 50-cm-long simple pendulum. Measure the distance from the center of the iOlab device to where the sting will be attached to its fixed point to be this \( 0.5 \mathrm{~m} \) length. You can make this fixed point by using sturdy tape to fix the string end to an edge of a table or shelf that will allow the device to swing freely below (see photo). Gorilla tape works really well if you have it, but duct tape or sturdy tape works also, or if there is a hook or nail available to tie to, that is fine as well.