(Solved): Two vertical forces, each of magnitude \( P=2.6 \) kips, are applied to a beam of the cross se ...

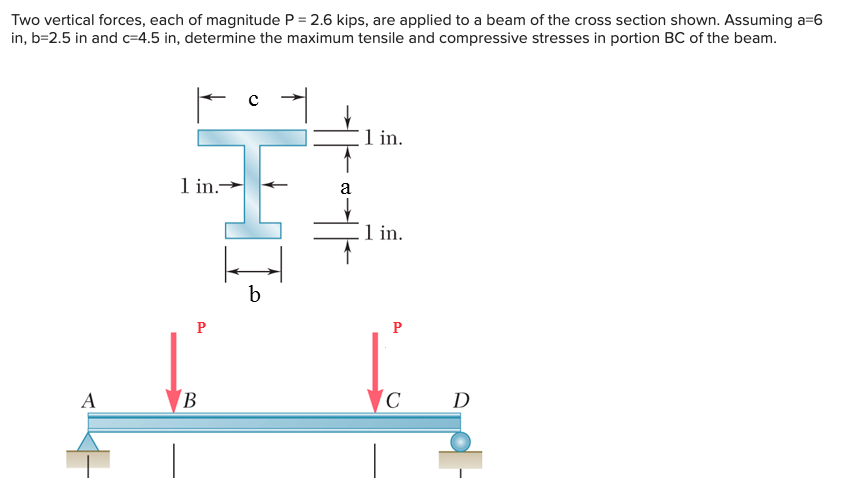
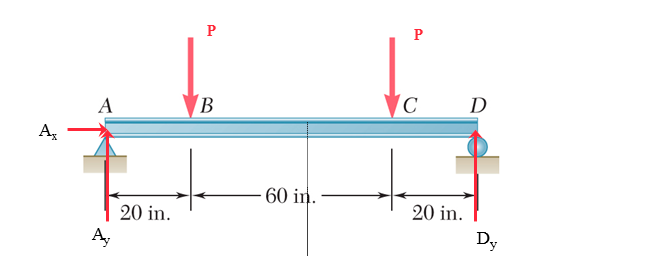
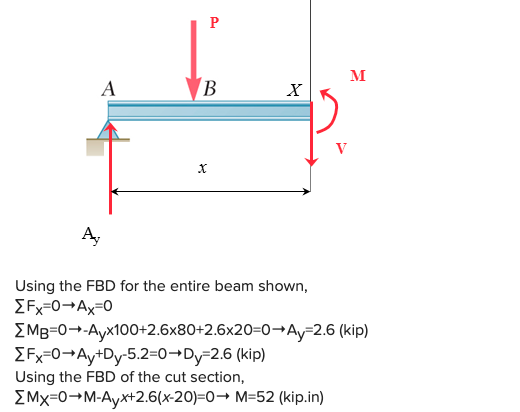
Two vertical forces, each of magnitude \( P=2.6 \) kips, are applied to a beam of the cross section shown. Assuming a \( =6 \) in, \( \mathrm{b}=2.5 \) in and \( \mathrm{c}=4.5 \mathrm{in} \), determine the maximum tensile and compressive stresses in portion \( \mathrm{BC} \) of the beam. Using the FBD for the entire beam shown, \( \sum F_{x}=0 \rightarrow A_{x}=0 \) \( \sum M_{B}=0 \rightarrow-A_{y} \times 100+2.6 \times 80+2.6 \times 20=0 \rightarrow A_{y}=2.6(k i p) \) \( \sum F_{x}=0 \rightarrow A_{y}+D_{y}-5.2=0 \rightarrow D_{y}=2.6(k i p) \) Using the \( F B D \) of the cut section, \[ \sum M_{X}=0 \rightarrow M_{-} A_{y} x+2.6(x-20)=0 \rightarrow M=52 \text { (kip.in) } \] 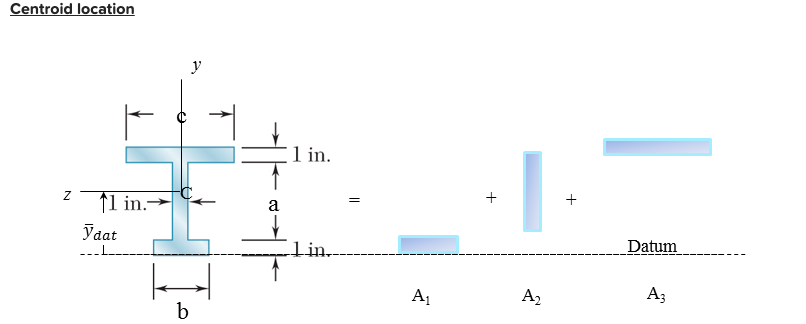Centroid location Subdividing the cross-section into the three simpler areas, \( A_{1}, A_{2} \& A_{3} \), shown \[ A_{1}=2.5 \mathrm{in}^{2}, A_{2}=6 \mathrm{in}^{2}, A_{3}=4.5 \mathrm{in}^{2} \] For the datum axis shown, \( \bar{y}_{\text {dat }}=\frac{\left(0.5 \times A_{1}+4 \times A_{2}+7.5 \times A_{3}\right)\left(i n^{3}\right)}{\left(A_{1}+A_{2}+A_{3}\right)\left(i n^{2}\right)}=4.538( \) in \( ) \) Moment of inertia The moment of inertia of area \( A_{1} \) about \( z \) axis is given as \( I_{Z 1}=\left((2.5) \times 1^{3}\right) / 12+A_{1} \times(4.038)^{2}=40.981\left(\right. \) in \( \left.{ }^{4}\right) \) The moment of inertia of area \( A_{2} \) about \( z \) axis is given as \( I_{Z 2}=\left((6)^{3} \times 1\right) / 12+A_{2} \times(0.538)^{2}=19.74\left(\right. \) in \( \left.{ }^{4}\right) \) The moment of inertia of area \( A_{3} \) about \( z \) axis is given as \( I_{Z 3}=\left((4.5) \times 1^{3}\right) / 12+A_{3} \times(-2.962)^{2}=39.843\left(\right. \) in \( \left.{ }^{4}\right) \) The moment of inertia of the entire cross-section, about the \( \mathrm{z} \) axis is given as \( \mathrm{I}_{\mathrm{z}}=\mathrm{I}_{\mathrm{z} 1}+\mathrm{I}_{\mathrm{z}} 2^{+\mathrm{I}_{\mathrm{z} 3}}=100.564\left(\mathrm{in}{ }^{4}\right. \) ) For the reaction moment \( M \), between \( B \) and \( C \), (i) the max. magnitude of the \( y \) coordinate on the (T) side is (in) and the max. magnitde of the (T) stress is (i) the max. magnitude of the \( y \) coordinate on the (C) side is (in) and the max. magnitude of the (C) stress is