Home /
Expert Answers /
Mechanical Engineering /
the-two-square-cross-sections-shown-below-figure-1-are-each-subjected-to-a-vertical-shear-force-v-pa185
(Solved): The two square cross sections shown below (Figure 1) are each subjected to a vertical shear force, V ...
The two square cross sections shown below (Figure 1) are
each subjected to a vertical shear force, V. The side length of
each cross section is s=5.75 in and the side length of the
hollowed-out portion of the second cross section is r=2.25 in
. The maximum allowable shear stress in each member is
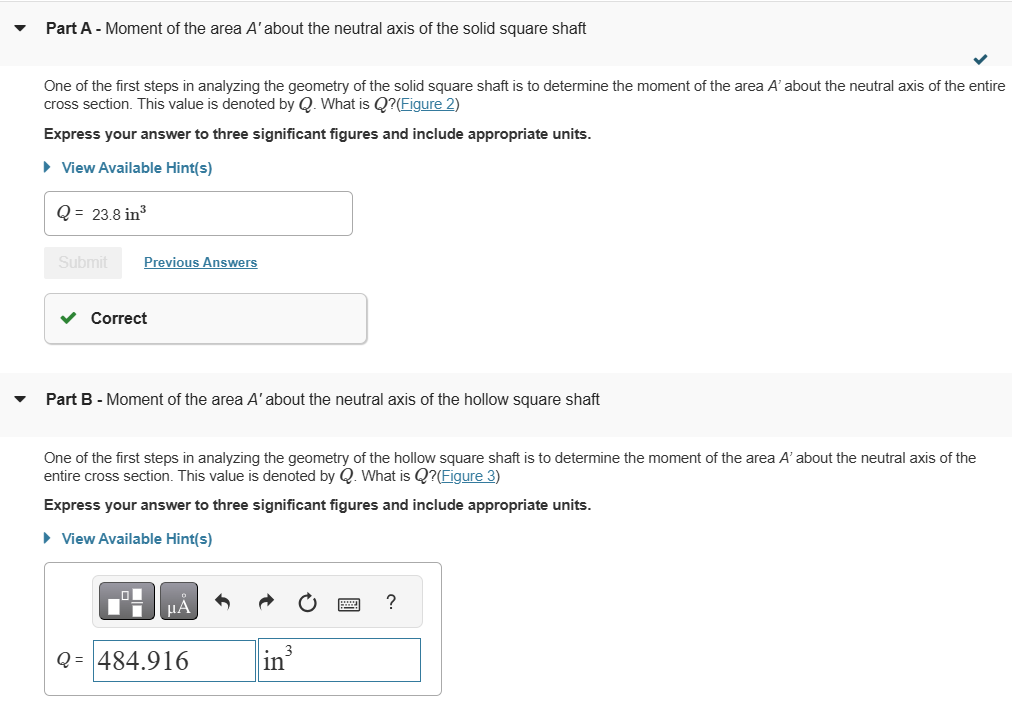
\tau _(max )=22.0ksi. Part A - Moment of the area A^(') about the neutral axis of the solid square shaft
One of the first steps in analyzing the geometry of the solid square shaft is to determine the moment of the area A^(') about the neutral axis of the entire
cross section. This value is denoted by Q. What is Q ? (Figure 2)
Express your answer to three significant figures and include appropriate units.
View Available Hint(s)
Part B - Moment of the area A^(') about the neutral axis of the hollow square shaft
One of the first steps in analyzing the geometry of the hollow square shaft is to determine the moment of the area A^(') about the neutral axis of the
entire cross section. This value is denoted by Q. What is Q ?(Figure 3)
Express your answer to three significant figures and include appropriate units.
View Available Hint(s)
Q=
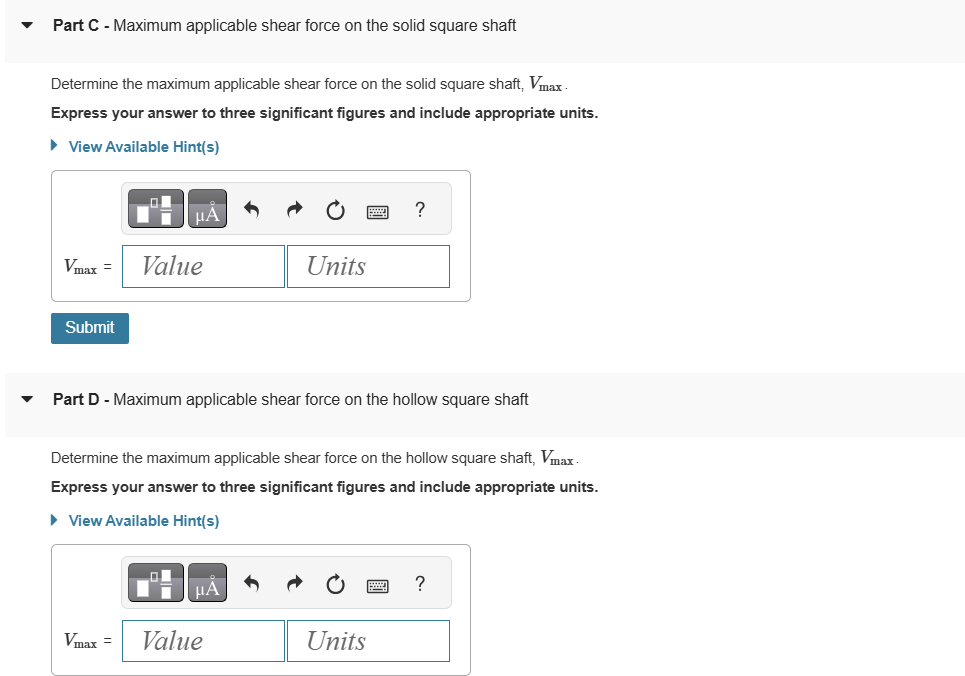
in^(3) Part C - Maximum applicable shear force on the solid square shaft
Determine the maximum applicable shear force on the solid square shaft, V_(max).
Express your answer to three significant figures and include appropriate units.
View Available Hint(s)
V_(max)=
Part D - Maximum applicable shear force on the hollow square shaft
Determine the maximum applicable shear force on the hollow square shaft, V_(max).
Express your answer to three significant figures and include appropriate units.
View Available Hint(s)
V_(max)=