(Solved): The three versions of the double-angle formula for cosine are given below. \[ \begin{array}{c} \cos ...

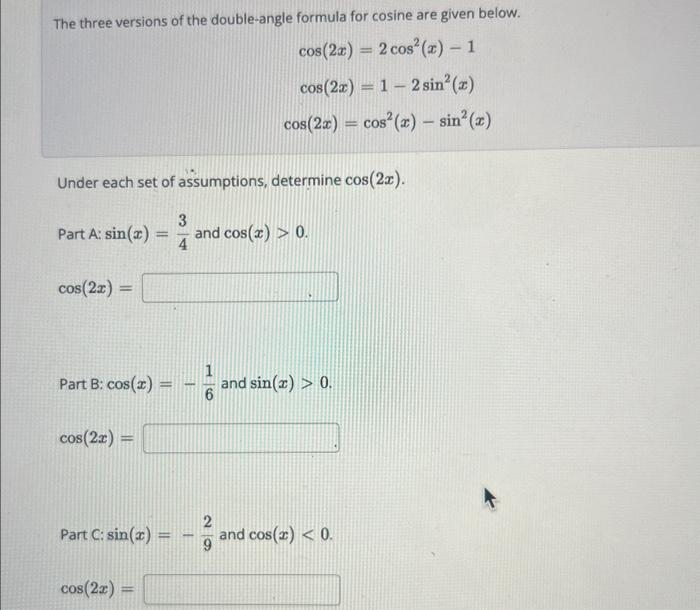
The three versions of the double-angle formula for cosine are given below. \[ \begin{array}{c} \cos (2 x)=2 \cos ^{2}(x)-1 \\ \cos (2 x)=1-2 \sin ^{2}(x) \\ \cos (2 x)=\cos ^{2}(x)-\sin ^{2}(x) \end{array} \] Under each set of assumptions, determine \( \cos (2 x) \). Part A: \( \sin (x)=\frac{3}{4} \) and \( \cos (x)>0 \) \[ \cos (2 x)= \] Part B: \( \cos (x)=-\frac{1}{6} \) and \( \sin (x)>0 \) \[ \cos (2 x)= \] \( \operatorname{Part} C: \sin (x)=-\frac{2}{9} \) and \( \cos (x)<0 \) \[ \cos (2 x)= \] Determine the value of \( \cos ^{2}(2 x)+\sin ^{2}(2 x) \). \[ \cos ^{2}(2 x)+\sin ^{2}(2 x)= \]