(Solved): The three freight cars are rolling along the horizontal track with the velocities shown. After the ...

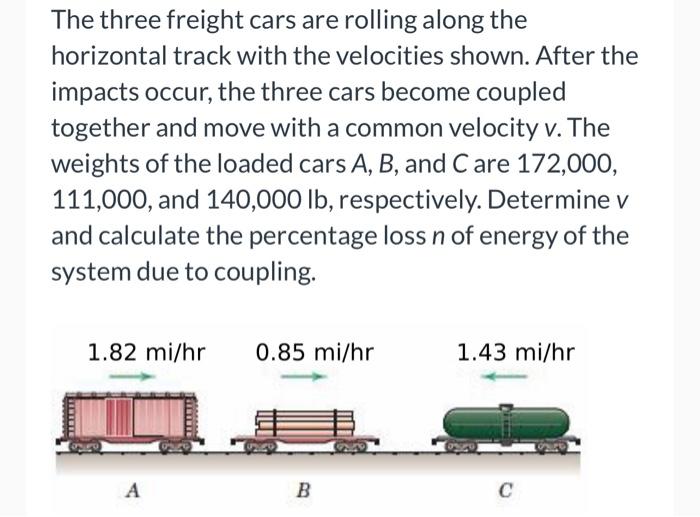
The three freight cars are rolling along the horizontal track with the velocities shown. After the impacts occur, the three cars become coupled together and move with a common velocity \( v \). The weights of the loaded cars \( A, B \), and \( C \) are 172,000, 111,000 , and 140,000 lb, respectively. Determine \( v \) and calculate the percentage loss \( n \) of energy of the system due to coupling. Solution: Apply momentum conservation: Let us assume that the velocity after impact becomes \( v \). \[ \begin{array}{l} \quad(189000 * 1.85+170000 * 1.40-197000 * 1.64) \frac{44}{30 * 32.2}=(189000+ \\ 170000+197000) \frac{44 v}{30 * 32.2} \\ \text { so } v=0.4758 \mathrm{mi} / \mathrm{hr} \\ \text { Now loss of Kinetic enery }=\mathrm{Ki}-\mathrm{Kf} \text { ki }=\text { Initial KE } \\ \text { Kf }=\text { final KE } \\ \text { so } \% \text { of loss of KE }=(\mathrm{Ki}-\mathrm{Kf}) / \mathrm{Ki}=(1-\mathrm{Kf} / \mathrm{Ki}) \\ \left(1-\frac{(189000+170000+197000) 0.4758^{2}}{189000 * 1.85^{2}+170000 * 1.40^{2}+197000 * 1.64^{2}}\right) 100 \\ =91.66 \% \text { loss } \end{array} \]