(Solved): The three basic trigonometric substitutions are in the table below. Part 1. Using the substitution: ...

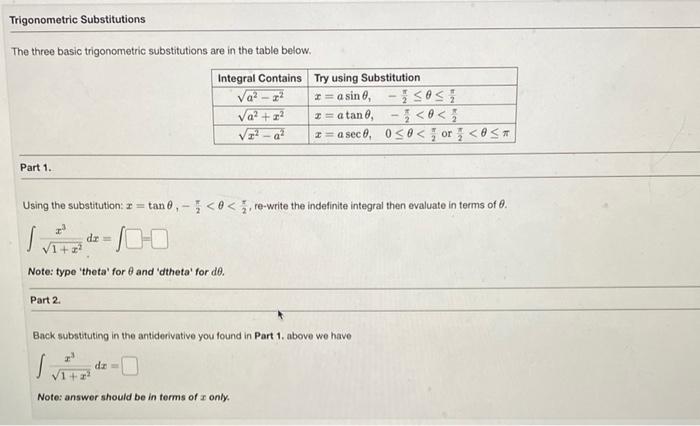
The three basic trigonometric substitutions are in the table below. Part 1. Using the substitution: \( x=\tan \theta,-\frac{\pi}{2}<\theta<\frac{\pi}{2} \), re-write the indefinite integral then evaluate in terms of \( \theta \). \[ \int \frac{x^{3}}{\sqrt{1+x^{2}}} d x=\int= \] Note: type 'theta' for \( \theta \) and 'dtheta' for de. Part 2. Back substituting in the antiderivative you found in Part 1. above we have \[ \int \frac{x^{3}}{\sqrt{1+x^{2}}} d x= \] Note: answer should be in terms of \( x \) only.