(Solved): The rable below gives for the value of continuous function \( f \) at each \( x \)-value. Using the ...

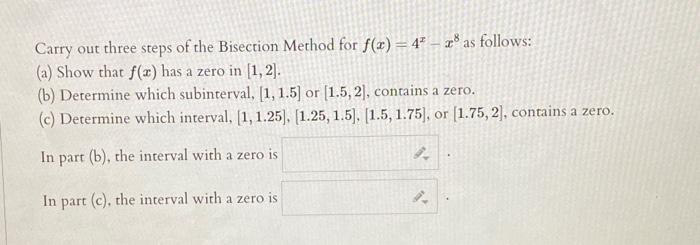
The rable below gives for the value of continuous function \( f \) at each \( x \)-value. Using the Intermediate Value Theorem and the information in the table, derermine the smallest interval in which the function must have a root. Carry out three steps of the Bisection Method for \( f(x)=4^{x}-x^{8} \) as follows: (a) Show that \( f(x) \) has a zero in \( [1,2] \). (b) Determine which subinterval, \( [1,1.5] \) or \( [1.5,2] \), contains a zero. (c) Determine which interval, \( [1,1.25],[1.25,1.5],[1.5,1.75] \), or \( [1.75,2] \), contains a zero. In part (b), the interval with a zero is In part (c), the interval with a zero is