Home /
Expert Answers /
Mechanical Engineering /
the-pressure-gradient-for-laminar-flow-through-a-tube-of-constant-radius-is-given-by-the-expression-pa367
(Solved): The pressure gradient for laminar flow through a tube of constant radius is given by the expression: ...
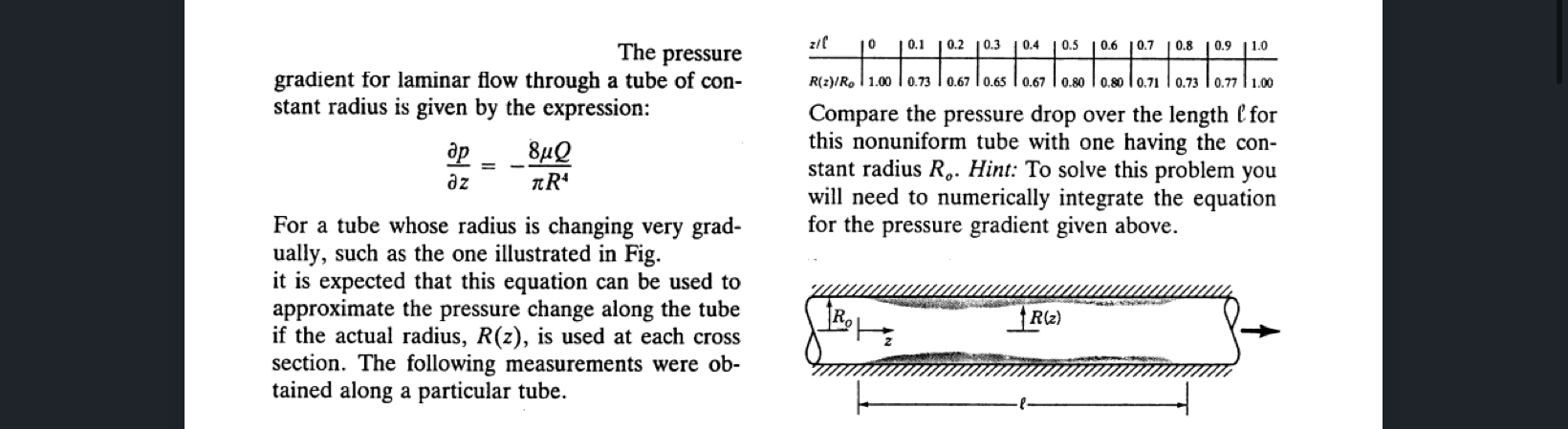
The pressure gradient for laminar flow through a tube of constant radius is given by the expression:
(delp)/(delz)=-(8\mu Q)/(\pi R^(4))For a tube whose radius is changing very gradually, such as the one illustrated in Fig. it is expected that this equation can be used to approximate the pressure change along the tube if the actual radius,
R(z), is used at each cross section. The following measurements were obtained along a particular tube. \table[[
(z)/(C),
^(0),0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0],[
R(z)/(R_(0)),1.00,0.73,0.67,0.65,0.67,0.80,0.80,0.71,0.73,0.77,1.00]] Compare the pressure drop over the length
lfor this nonuniform tube with one having the constant radius
R_(o). Hint: To solve this problem you will need to numerically integrate the equation for the pressure gradient given above.