(Solved): The model symbol of an op amp is shown in the figure above. Recall from MAE 376, due to the high in ...

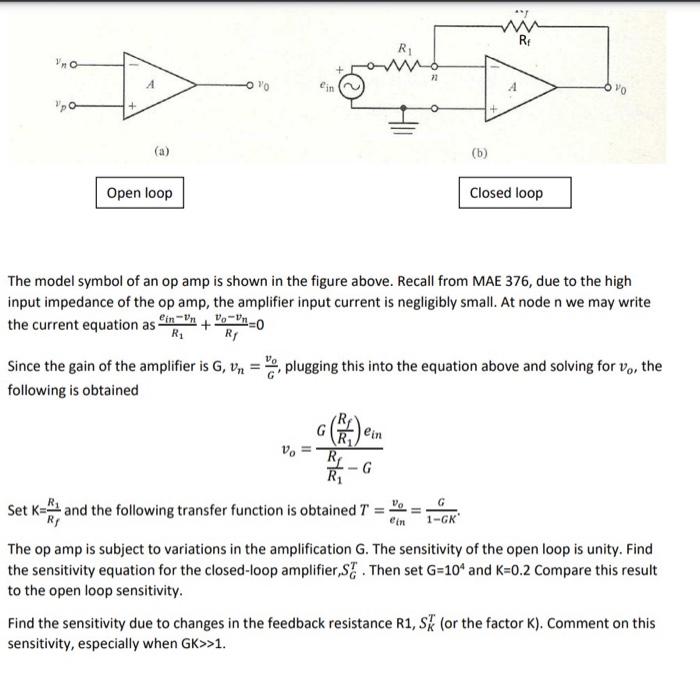
The model symbol of an op amp is shown in the figure above. Recall from MAE 376, due to the high input impedance of the op amp, the amplifier input current is negligibly small. At node \( n \) we may write the current equation as \( \frac{e_{i n}-v_{n}}{R_{1}}+\frac{v_{0}-v_{n}}{R_{f}}=0 \) Since the gain of the amplifier is G, \( v_{n}=\frac{v_{o}}{G} \), plugging this into the equation above and solving for \( v_{0} \), the following is obtained \[ v_{o}=\frac{G\left(\frac{R_{f}}{R_{1}}\right) e_{i n}}{\frac{R_{f}}{R_{1}}-G} \] Set \( \mathrm{K}=\frac{R_{1}}{R_{f}} \) and the following transfer function is obtained \( T=\frac{v_{o}}{e_{i n}}=\frac{G}{1-G K} \). The op amp is subject to variations in the amplification \( \mathrm{G} \). The sensitivity of the open loop is unity. Find the sensitivity equation for the closed-loop amplifier, \( S_{G}^{T} \). Then set \( \mathrm{G}=10^{4} \) and \( \mathrm{K}=0.2 \mathrm{Compare} \) this result to the open loop sensitivity. Find the sensitivity due to changes in the feedback resistance R1, \( S_{K}^{T} \) (or the factor \( \mathrm{K} \) ). Comment on this sensitivity, especially when \( G K \gg>1 \).