(Solved): The figure below shows the graph of a rational function \( f \). It has vertical asymptotes \( x=2 ...

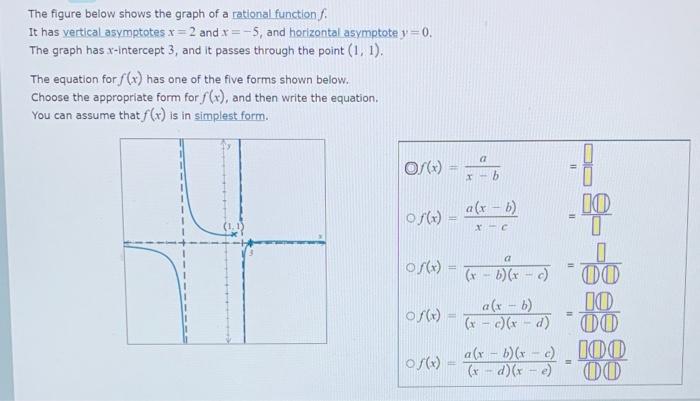
The figure below shows the graph of a rational function \( f \). It has vertical asymptotes \( x=2 \) and \( x=-5 \), and horizontal asymptote \( y=0 \). The graph has \( x \)-intercept 3 , and it passes through the point \( (1,1) \). The equation for \( f(x) \) has one of the five forms shown below. Choose the appropriate form for \( f(x) \), and then write the equation. You can assume that \( f(x) \) is in simplest form. \[ \begin{array}{l} f(x)=\frac{a}{x-b}= \\ f(x)=\frac{a(x-b)}{x-c} \\ f(x)=\frac{a}{(x-b)(x-c)}=\frac{10(1)}{0} \\ f(x)=\frac{a(x-b)}{(x-c)(x-d)}=\frac{\square(0)}{(\square 00)} \\ f(x)=\frac{a(x-b)(x-c)}{(x-d)(x-c)}=\frac{\square(0)(])}{(0)(\square)} \\ \end{array} \]