(Solved): The doubly-symmetric cross-section shown has principal axes in the \( y \) - and \( z \)-direction ...

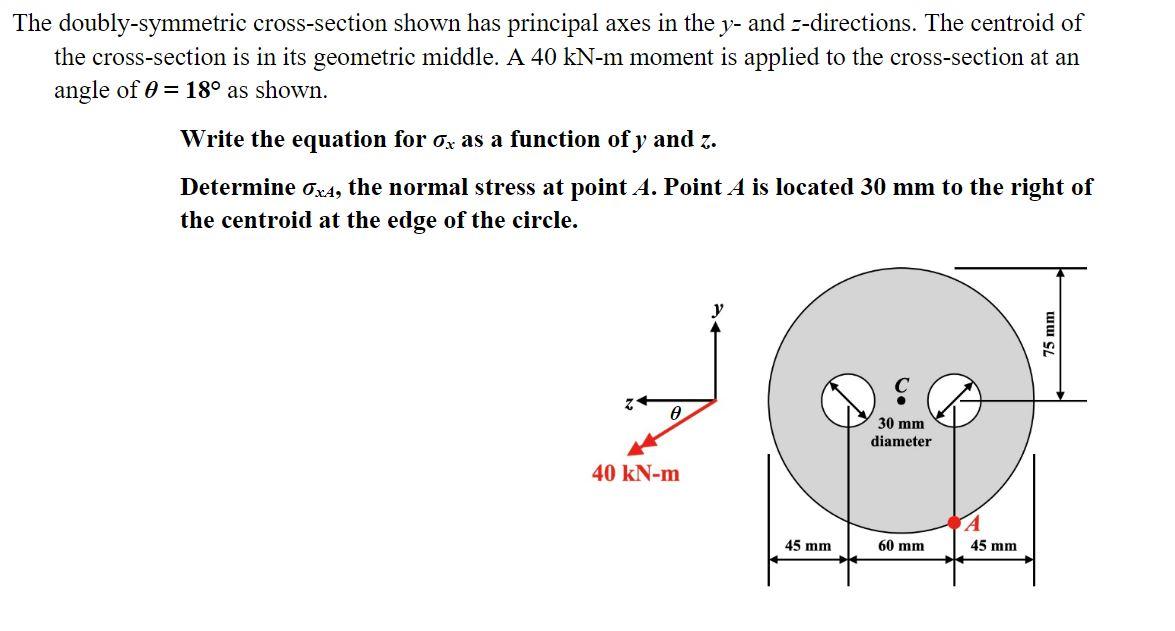
The doubly-symmetric cross-section shown has principal axes in the \( y \) - and \( z \)-directions. The centroid of the cross-section is in its geometric middle. A \( 40 \mathrm{kN}-\mathrm{m} \) moment is applied to the cross-section at an angle of \( \theta=18^{\circ} \) as shown. Write the equation for \( \sigma_{x} \) as a function of \( y \) and \( z \). Determine \( \sigma_{x A} \), the normal stress at point \( A \). Point \( A \) is located \( 30 \mathrm{~mm} \) to the right of the centroid at the edge of the circle.