(Solved): The double-angle formula for sine is given below. \[ \sin (2 x)=2 \sin (x) \cos (x) \] In In-Class ...

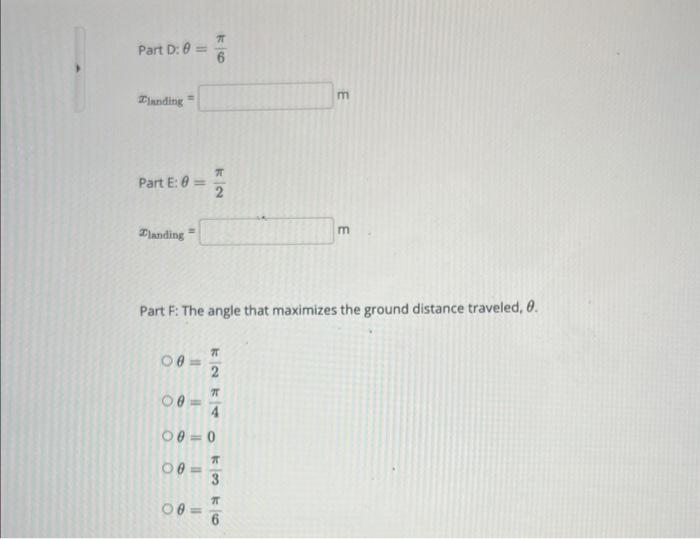
The double-angle formula for sine is given below. \[ \sin (2 x)=2 \sin (x) \cos (x) \] In In-Class Activity 11.A, we used the following equations to model the motion of the potato launched by the cannon. \[ \begin{array}{c} x=t_{0} \cos (\theta) t \\ h=v \sin (\theta) t-\frac{1}{2} g t^{2} \end{array} \] \[ \text { Tlanding }=\frac{v_{0}^{2}}{g} \sin (2 \theta) \] to is the initial velocity, \( \theta \) is the launch angle, \( g \) is the acceleration due to gravity \( \left(9.81 \mathrm{~m} / \mathrm{s}^{2}\right) \), and \( x_{\text {landing }} \), refers to the horizontal distance traveled by the potato (after it returns to the ground). A potato is launched from a potato canon with an initial velocity of \( v_{0}=900 \mathrm{~m} / 5 \). Determine the horizontal distance, \( x_{\text {landing }} \) that the projectile travels with the following launch angles, \( \theta \). Part \( \mathrm{A}: \theta=0 \) Part D: \( \theta=\frac{\pi}{6} \) \( x_{\text {landing }}= \) \( \operatorname{Part} \mathrm{E}: \theta=\frac{\pi}{2} \) \( x_{\text {landing }}= \) Part F: The angle that maximizes the ground distance traveled, \( \theta \). \( \theta=\frac{\pi}{2} \) \( \theta=\frac{\pi}{4} \) \( \theta=0 \) \( \theta=\frac{\pi}{3} \) \( \theta=\frac{\pi}{6} \) Assume \( \cos (x)=\frac{1}{6} \) and \( \sin (x)<0 \). Part A: Determine the value of \( c \) in the diagram shown. \[ c= \] Part B: Determine the value of \( b \) in the diagram shown. Write your answer in exact form. Part C: Determine the value of \( \sin (x) \). Write your answer in exact form. \[ \sin (x)= \] Part D: Use the double-angle formula to determine \( \sin (2 x) \). Write your answer in exact form. 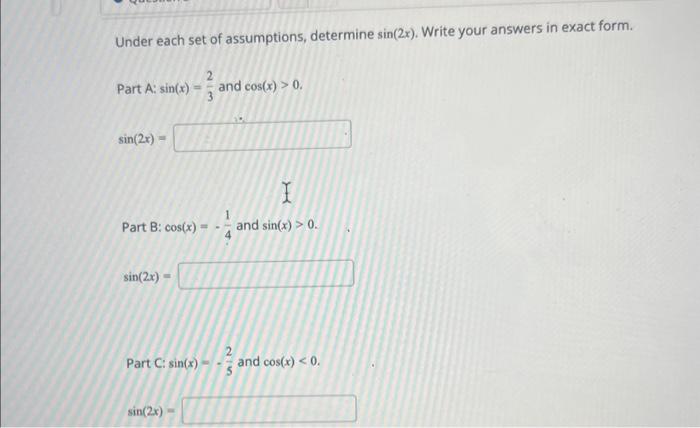\[ \sin (2 x)= \] Under each set of assumptions, determine \( \sin (2 x) \). Write your answers in exact form. Part A: \( \sin (x)=\frac{2}{3} \) and \( \cos (x)>0 \). \[ \sin (2 x)= \] Part B: \( \cos (x)=-\frac{1}{4} \) and \( \sin (x)>0 \). \[ \sin (2 x)= \] Part C: \( \sin (x)=-\frac{2}{5} \) and \( \cos (x)<0 \). \[ \sin (2 x)= \]