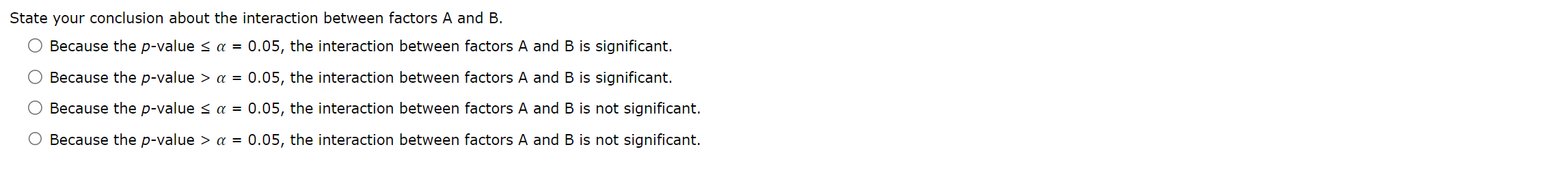(Solved): The calculations for a factorial experiment involving four levels of factor A, three levels of facto ...

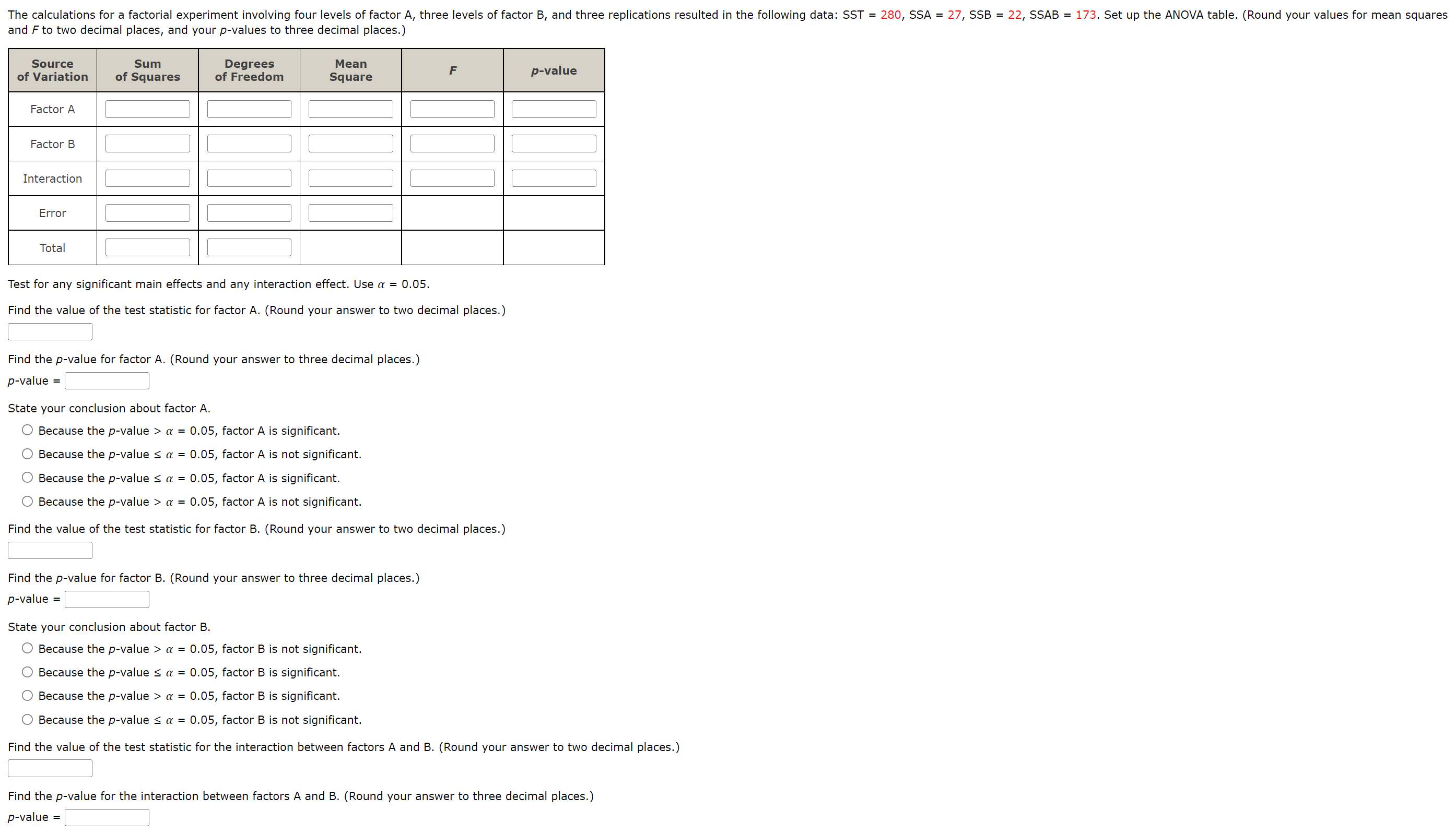
The calculations for a factorial experiment involving four levels of factor A, three levels of factor B, and three replications resulted in the following data: SST = 280, SSA = 27, SSB = 22, SSAB = 173. Set up the ANOVA table. (Round your values for mean squares and F to two decimal places, and your p-values to three decimal places.)

and \( F \) to two decimal places, and your \( p \)-values to three decimal places.) Test for any significant main effects and any interaction effect. Use \( \alpha=0.05 \). Find the value of the test statistic for factor \( A \). (Round your answer to two decimal places.) Find the \( p \)-value for factor \( \mathrm{A} \). (Round your answer to three decimal places.) \( p \)-value \( = \) State your conclusion about factor \( \mathrm{A} \). Because the \( p \)-value \( >\alpha=0.05 \), factor \( \mathrm{A} \) is significant. Because the \( p \)-value \( \leq \alpha=0.05 \), factor \( \mathrm{A} \) is not significant. Because the \( p \)-value \( \leq \alpha=0.05 \), factor \( \mathrm{A} \) is significant. Because the \( p \)-value \( >\alpha=0.05 \), factor \( \mathrm{A} \) is not significant. Find the value of the test statistic for factor \( B \). (Round your answer to two decimal places.) Find the \( p \)-value for factor \( B \). (Round your answer to three decimal places.) \( p \)-value \( = \) State your conclusion about factor \( B \). Because the \( p \)-value \( >\alpha=0.05 \), factor \( \mathrm{B} \) is not significant. Because the \( p \)-value \( \leq \alpha=0.05 \), factor \( B \) is significant. Because the \( p \)-value \( >\alpha=0.05 \), factor \( \mathrm{B} \) is significant. Because the \( p \)-value \( \leq \alpha=0.05 \), factor \( \mathrm{B} \) is not significant. Find the value of the test statistic for the interaction between factors \( A \) and \( B \). (Round your answer to two decimal places.) Find the \( p \)-value for the interaction between factors \( A \) and \( B \). (Round your answer to three decimal places.) State your conclusion about the interaction between factors \( A \) and \( B \). Because the \( p \)-value \( \leq \alpha=0.05 \), the interaction between factors \( \mathrm{A} \) and \( \mathrm{B} \) is significant. Because the \( p \)-value \( >\alpha=0.05 \), the interaction between factors \( \mathrm{A} \) and \( \mathrm{B} \) is significant. Because the \( p \)-value \( \leq \alpha=0.05 \), the interaction between factors \( \mathrm{A} \) and \( \mathrm{B} \) is not significant. Because the \( p \)-value \( >\alpha=0.05 \), the interaction between factors \( \mathrm{A} \) and \( \mathrm{B} \) is not significant.