(Solved): Suppose that the heart beat per minute (bpm) of adult males has a normal distribution with a mean o ...

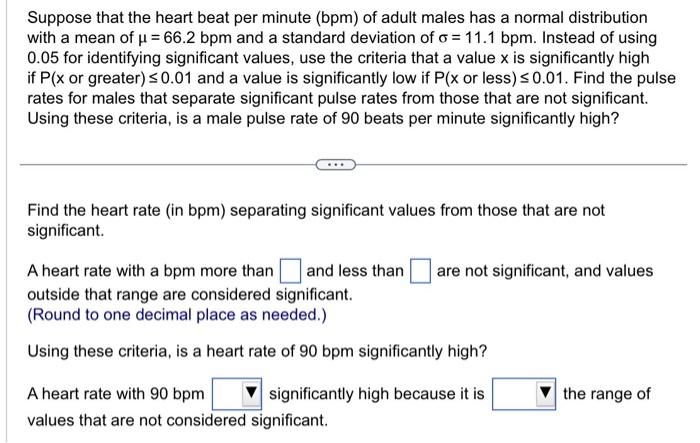
Suppose that the heart beat per minute (bpm) of adult males has a normal distribution with a mean of \( \mu=66.2 \mathrm{bpm} \) and a standard deviation of \( \sigma=11.1 \mathrm{bpm} \). Instead of using \( 0.05 \) for identifying significant values, use the criteria that a value \( \mathrm{x} \) is significantly high if \( \mathrm{P}(\mathrm{x} \) or greater \( ) \leq 0.01 \) and a value is significantly low if \( \mathrm{P}(\mathrm{x} \) or less \( ) \leq 0.01 \). Find the pulse rates for males that separate significant pulse rates from those that are not significant. Using these criteria, is a male pulse rate of 90 beats per minute significantly high? Find the heart rate (in bpm) separating significant values from those that are not significant. A heart rate with a bpm more than and less than are not significant, and values outside that range are considered significant. (Round to one decimal place as needed.) Using these criteria, is a heart rate of \( 90 \mathrm{bpm} \) significantly high? A heart rate with \( 90 \mathrm{bpm} \) significantly high because it is the range of values that are not considered significant.