(Solved): Suppose \( \mathbf{a}_{1}, \mathbf{a}_{2}, \mathbf{a}_{3}, \mathbf{a}_{4} \), and \( \mathbf{a}_{5} ...

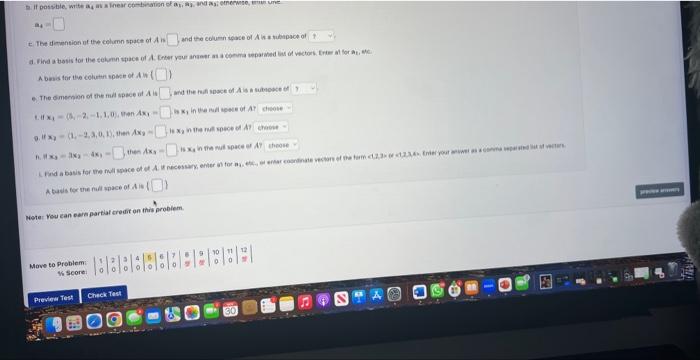
Suppose \( \mathbf{a}_{1}, \mathbf{a}_{2}, \mathbf{a}_{3}, \mathbf{a}_{4} \), and \( \mathbf{a}_{5} \) are vectors in \( \mathbb{R}^{3}, A=\left(\mathbf{a}_{1}\left|\mathbf{a}_{2}\right| \mathbf{a}_{3}\left|\mathbf{a}_{4}\right| \mathbf{a}_{5}\right) \), and \[ \operatorname{rref}(A)=\left[\begin{array}{ccccc} 1 & 0 & 0 & -5 & -1 \\ 0 & 1 & 0 & 2 & 2 \\ 0 & 0 & 1 & 1 & -3 \end{array}\right] \] a. Select all of the true statements (there may be more than one correct answer). A. \( \left\{\mathbf{a}_{1}, \mathbf{a}_{2}, \mathbf{a}_{3}, \mathbf{a}_{4}\right\} \) is a linearly independent set B. \( \left\{\mathbf{a}_{1}, \mathbf{a}_{2}, \mathbf{a}_{3}\right\} \) is a basis for \( \mathbb{R}^{3} \) C. \( \left\{\mathbf{a}_{1}, \mathbf{a}_{2}\right\} \) is a linearly independent set D. \( \operatorname{span}\left\{\mathbf{a}_{1}, \mathbf{a}_{2}\right\}=\mathbb{R}^{3} \) E. \( \operatorname{span}\left\{\mathbf{a}_{1}, \mathbf{a}_{2}, \mathbf{a}_{3}\right\}=\mathbb{R}^{3} \) F. \( \left\{\mathbf{a}_{1}, \mathbf{a}_{2}\right\} \) is a basis for \( \mathbb{R}^{3} \). G. \( \left\{a_{1}, a_{2}, a_{3}, a_{4}\right\} \) is a basis for \( \mathbb{R}^{3} \). H. \( \operatorname{span}\left\{\mathbf{a}_{1}, \mathbf{a}_{2}, \mathbf{a}_{3}, \mathbf{a}_{4}\right\}=\mathbb{R}^{3} \) 1. \( \left\{a_{1}, a_{2}, a_{3}\right\} \) is a linearly independent set b. If possible, write \( \mathbf{a}_{4} \) as a linear combination of \( \mathbf{a}_{1}, \mathbf{a}_{2} \), and \( \mathbf{a}_{3} \); otherwise, enter DNE. \[ a_{4}= \] c. The dimension of the column space of \( A \) is and the column space of \( A \) is a subspace of d. Find a basis for the column space of \( A \). Enter your answer as a comma separated list of vectors. Enter a1 for \( a_{1} \), etc. A basis for the column space of \( A \) is \{\} e. The dimension of the null space of \( A \) is and the null space of \( A \) is a subspace of f. If \( \mathrm{x}_{1}=\langle 5,-2,-1,1,0\rangle \), then \( A \mathrm{x}_{1}= \) Is \( \mathrm{x}_{1} \) in the null space of \( A \) ? t. The dinwention ut the column space of \( A \) is and the colunn space of \( A \) is a nubapsce of A bwis tor tive colutin spese of \( A \) in ? 6. The ememien of the mit spece of \( A \) is and the fan sosce of \( A \) is on sumoske of A bads for the fail wace of \( A \) is 1 Wote: Vou can cova partiaf credit on thin probiem. \begin{tabular}{|c|c|c|c|c|c|c|c|c|c|c|c|c|} Mave to Problem: & 1 & 2 & 3 & 4 & 5 & 5 & 7 & 5 & 9 & 10 & 11 & 12 \\ Ws scorei & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \( y \) & 4 & 0 & 0 & \( =1 \) \end{tabular}