(Solved): SOLVE FOR SHEAR STRESS MAX USING MOHRS CIRCLE (As Shown Blank)!!! The values in the first ...

SOLVE FOR SHEAR STRESS MAX USING MOHR’S CIRCLE (As Shown Blank)!!!
The values in the first image, having normal stresses, are correct! 
PLEASE SOLVE FOR THE SECOND IMAGE ONLY, thank you.
PLEASE DO NOT REPLY WITH INCORRECT ANSWERS, double check calculations, AND BE AS DETAILED AS POSSIBLE!!!

Also, please,write the functions in the same way that they appear in the question so that I can understand what is written.

A cantilevered beam is loaded as shown. The cross section at the wall is shown, with points of interest \( A \) (at the top), \( B \) (at the center), and \( C \) (midway between \( A \) and \( B \) ). where \( F=2.8 \mathrm{kN} \) NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. Calculate the magnitudes of the stresses acting on the stress elements. Do not neglect transverse shear stress. 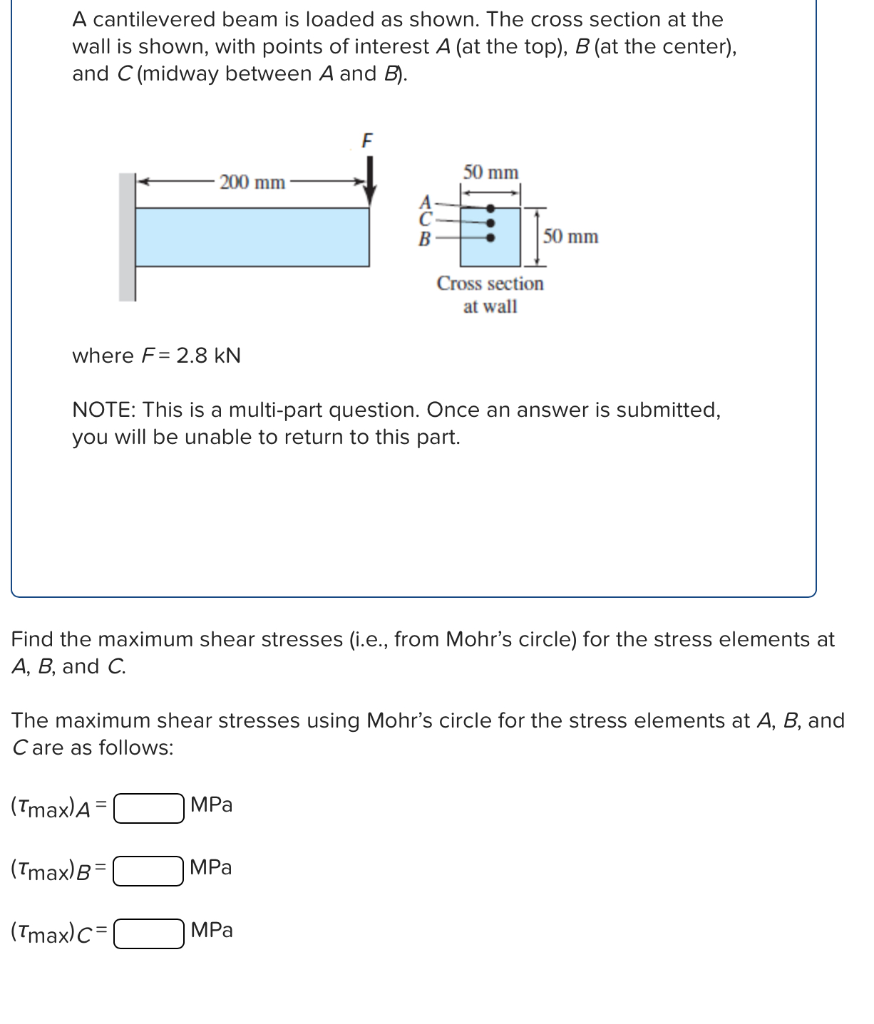The magnitude of stresses acting on the stress elements are as follows: At element \( A \), \( \sigma_{A}=\quad \mathrm{MPa} \) and \( \tau_{A}=\quad \mathrm{MPa} \) At element B, \( \sigma_{B}=\quad \mathrm{MPa} \) and \( \tau_{B}=\quad \mathrm{MPa} \) At element \( \mathrm{C} \), \( \sigma_{C}=\quad \mathrm{MPa} \) and \( \mathrm{T}_{C}=\quad \mathrm{MPa} \) A cantilevered beam is loaded as shown. The cross section at the wall is shown, with points of interest \( A \) (at the top), \( B \) (at the center), and \( C \) (midway between \( A \) and \( B \) ). where \( F=2.8 \mathrm{kN} \) NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. Find the maximum shear stresses (i.e., from Mohr's circle) for the stress elements at \( A, B \), and \( C \). The maximum shear stresses using Mohr's circle for the stress elements at \( A, B \), and Care as follows: \( \left(\tau_{\max }\right)^{2}=\quad \mathrm{MPa} \) \( \left(\tau_{\max }\right)^{=} \quad \mathrm{MPa} \) \( \left(\tau_{\max }\right)^{=} \quad \mathrm{MPa} \)