(Solved): Seatwork 1. Measurement of op amp CMRR. The standard way to measure the common-mode rejection rati ...

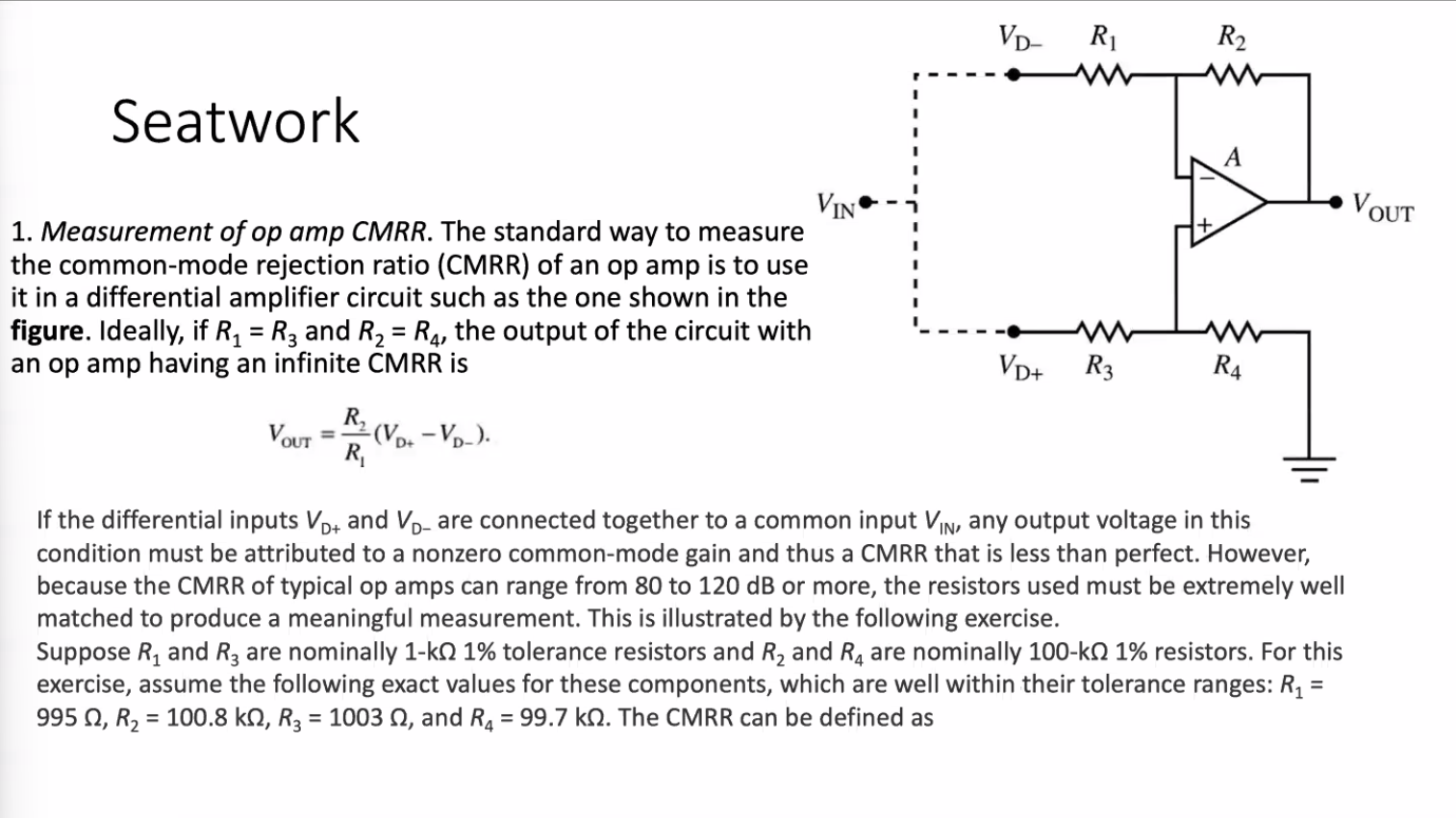
Seatwork 1. Measurement of op amp CMRR. The standard way to measure the common-mode rejection ratio (CMRR) of an op amp is to ust it in a differential amplifier circuit such as the one shown in the figure. Ideally, if \( R_{1}=R_{3} \) and \( R_{2}=R_{4} \), the output of the circuit witl an op amp having an infinite CMRR is \[ V_{\text {OUT }}=\frac{R_{2}}{R_{1}}\left(V_{\mathrm{D}_{+}}-V_{\mathrm{D}-}\right) . \] If the differential inputs \( V_{\mathrm{D}^{+}} \)and \( V_{\mathrm{D}-} \) are connected together to a common input \( V_{\mathbb{N}} \), any output voltage in this condition must be attributed to a nonzero common-mode gain and thus a CMRR that is less than perfect. However, because the CMRR of typical op amps can range from 80 to \( 120 \mathrm{~dB} \) or more, the resistors used must be extremely well matched to produce a meaningful measurement. This is illustrated by the following exercise. Suppose \( R_{1} \) and \( R_{3} \) are nominally \( 1-k \Omega 1 \% \) tolerance resistors and \( R_{2} \) and \( R_{4} \) are nominally \( 100-k \Omega 1 \% \) resistors. For this exercise, assume the following exact values for these components, which are well within their tolerance ranges: \( R_{1}= \) \( 995 \Omega, R_{2}=100.8 \mathrm{k} \Omega, R_{3}=1003 \Omega \), and \( R_{4}=99.7 \mathrm{k} \Omega \). 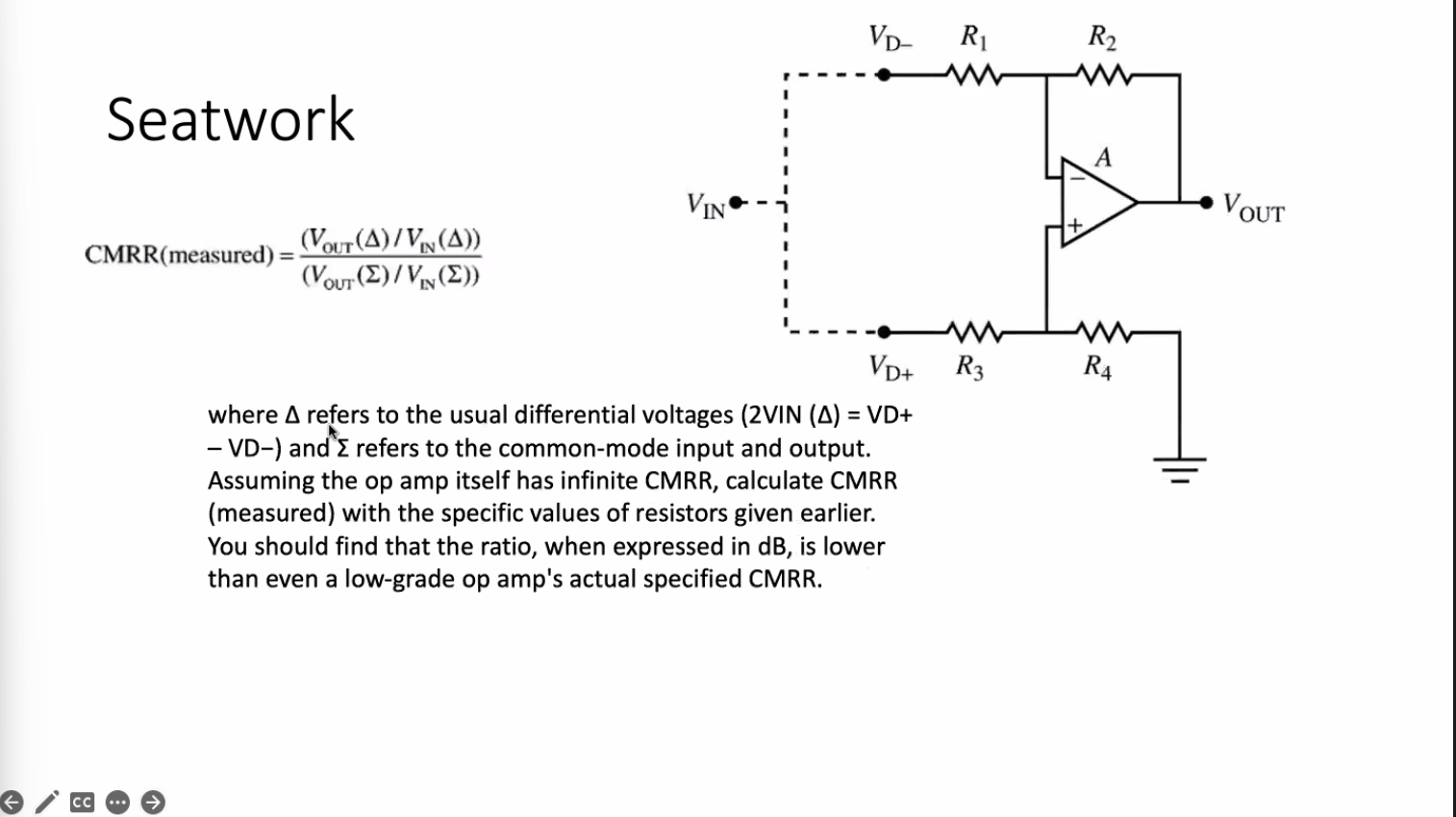The CMRR can be defined as Seatwork \[ \operatorname{CMRR}(\text { measured })=\frac{\left(V_{\mathrm{OUT}}(\Delta) / V_{\mathrm{IV}}(\Delta)\right)}{\left(V_{\mathrm{OUT}}(\Sigma) / V_{\mathrm{IN}}(\Sigma)\right)} \] where \( \Delta \) refers to the usual differential vi - VD-) and \( \Sigma \) refers to the common-mod? Assuming the op amp itself has infinite CMRK, calculate CMRR (measured) with the specific values of resistors given earlier. You should find that the ratio, when expressed in \( \mathrm{dB} \), is lower than even a low-grade op amp's actual specified CMRR.