(Solved): Required information An excellent approximation for the two-dimensional incompressible laminar bou ...

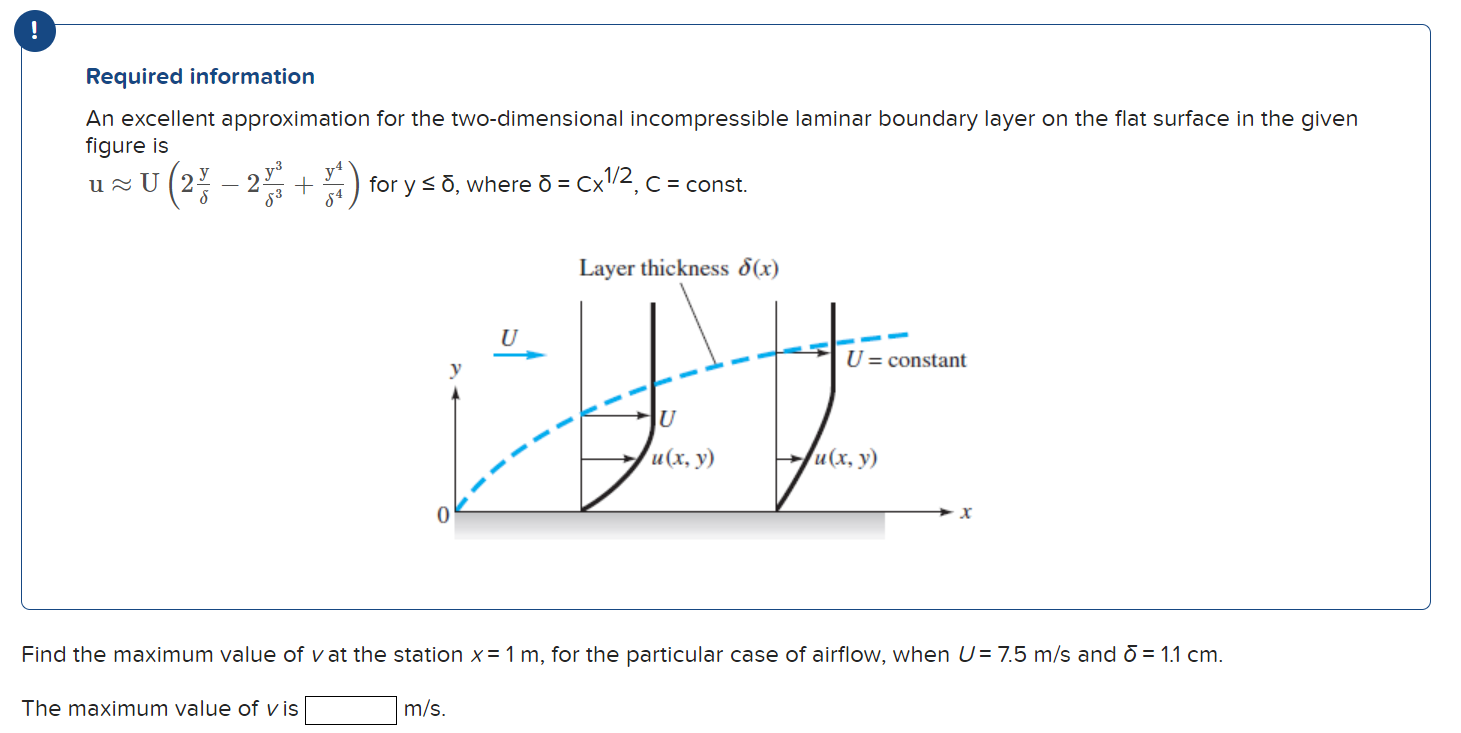
Required information An excellent approximation for the two-dimensional incompressible laminar boundary layer on the flat surface in the given figure is \( \mathrm{u} \approx \mathrm{U}\left(2 \frac{\mathrm{y}}{\delta}-2 \frac{\mathrm{y}^{3}}{\delta^{3}}+\frac{\mathrm{y}^{4}}{\delta^{4}}\right) \) for \( \mathrm{y} \leq \overline{\mathrm{o}} \), where \( \bar{o}=\mathrm{Cx}{ }^{1 / 2}, \mathrm{C}= \) const. Find the maximum value of \( v \) at the station \( x=1 \mathrm{~m} \), for the particular case of airflow, when \( U=7.5 \mathrm{~m} / \mathrm{s} \) and \( \delta=1.1 \mathrm{~cm} \). The maximum value of \( v \) is \( \quad \mathrm{m} / \mathrm{s} \).