(Solved): Problem Three: Stacking Cans On a recent trip to grocery store, I saw a bunch of cans stacked up ...

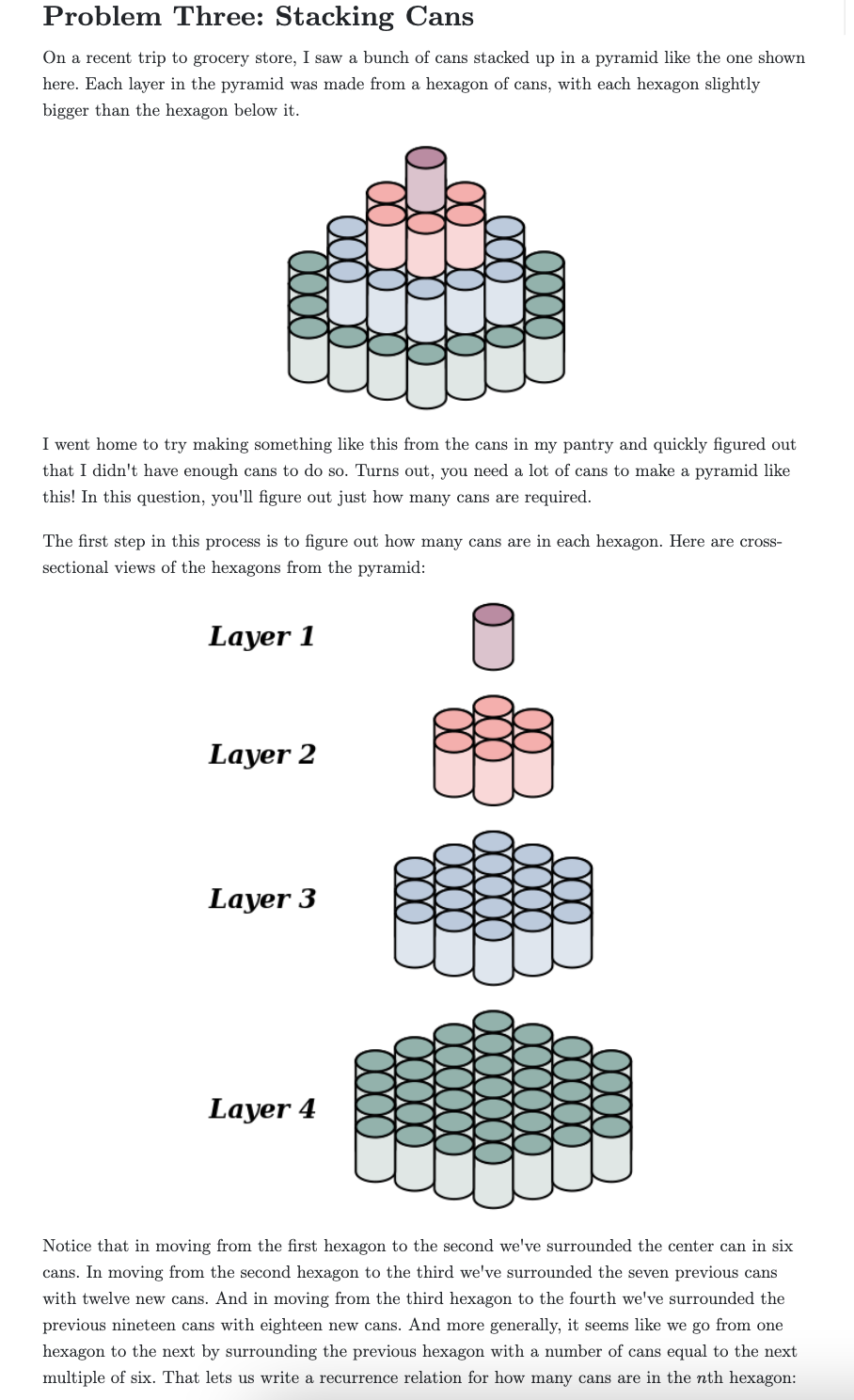
Problem Three: Stacking Cans On a recent trip to grocery store, I saw a bunch of cans stacked up in a pyramid like the one shown here. Each layer in the pyramid was made from a hexagon of cans, with each hexagon slightly bigger than the hexagon below it. 000 WD D Coco a 200 COO a a I went home to try making something like this from the cans in my pantry and quickly figured out that I didn't have enough cans to do so. Turns out, you need a lot of cans to make a pyramid like this! In this question, you'll figure out just how many cans are required. The first step in this process is to figure out how many cans are in each hexagon. Here are cross- sectional views of the hexagons from the pyramid: Layer 1 8 Layer 2 Layer 3 000 C000 2000 000 COO00 Layer 4 Notice that in moving from the first hexagon to the second we've surrounded the center can in six cans. In moving from the second hexagon to the third we've surrounded the seven previous cans with twelve new cans. And in moving from the third hexagon to the fourth we've surrounded the previous nineteen cans with eighteen new cans. And more generally, it seems like we go from one hexagon to the next by surrounding the previous hexagon with a number of cans equal to the next multiple of six. That lets us write a recurrence relation for how many cans are in the nth hexagon: h? = 1 n+1= n + 6n. Pause for a minute to make sure you see why this is. i. Prove by induction that hn = 3n(n-1) + 1 for all natural numbers n > 1. As in Problem Two, you begin here with the recursive definition of h given above, then need to show that the terms of the series are also given by the simpler formula 3n(n-1) +1. Now that we know how many cans are in each hexagon, we can start working out how many cans it takes to make a pyramid with n layers. ii. Fill in the following blanks. No justification is required. (This is for the whole tower, not the largest layer only.) O A 1-layer tower has 1 can in it. 0 A 2-layer tower has cans in it. O A 3-layer tower has cans in it. o A 4-layer tower has cans in it. o A 5-layer tower has cans in it. 0 A 6-layer tower has cans in it. O A 7-layer tower has cans in it. A 8-layer tower has cans in it. A 9-layer tower has cans in it. A 10-layer tower has cans in it. o o o iii. Fill in the following blank with a simple mathematical expression (e.g. n+ 19n +1, Vn2 +5, [3]”, etc, but not a recurrence relation like tn+1 = tn + hn+1). No justification is required. An n-layer tower has cans in it. (Remember, this is the total for the whole tower.) iv. Prove by induction on n that your formula from part (iii) holds for all natural numbers n. We've asked you to prove this is true for all natural numbers n, including when n=0. Your answer to part (iv) explains why I wasn't able to build any reasonable pyramid from the cans I have at home. It's worth taking a minute or two to ponder how much it would cost to build a pyramid twenty layers deep! A purely optional but very rewarding question to ponder: the formula you proved correct in part (iv) suggests there's a completely different way to arrange the cans in the pyramid into an appealing geometrical shape. What is that other shape? Can you find a way to explain why that shape - which superficially has nothing to do with hexagons - relates back to hexagonal layers?