(Solved): Problem 2. Fourier Transform of a Periodic Signal Consider the periodic signal of Figure 2 : Figur ...

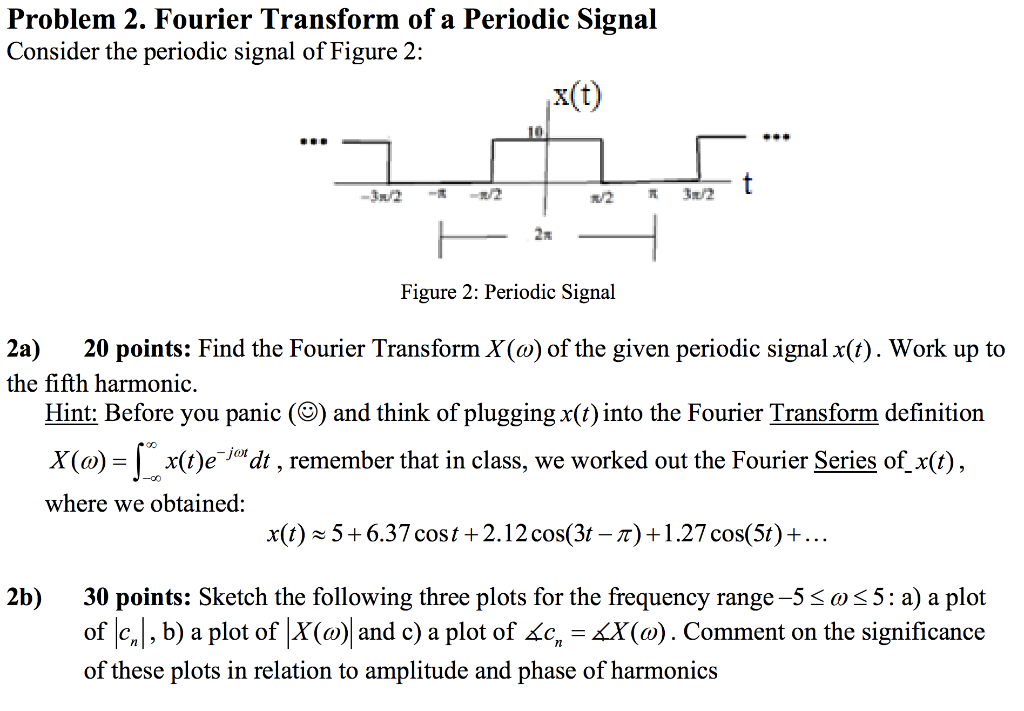
Problem 2. Fourier Transform of a Periodic Signal Consider the periodic signal of Figure 2 : Figure 2: Periodic Signal 2a) 20 points: Find the Fourier Transform \( X(\omega) \) of the given periodic signal \( x(t) \). Work up to the fifth harmonic. Hint: Before you panic (()) and think of plugging \( x(t) \) into the Fourier Transform definition \( X(\omega)=\int_{-\infty}^{\infty} x(t) e^{-j \omega t} d t \), remember that in class, we worked out the Fourier Series of \( x(t) \), where we obtained: \[ x(t) \approx 5+6.37 \cos t+2.12 \cos (3 t-\pi)+1.27 \cos (5 t)+\ldots \] 2b) 30 points: Sketch the following three plots for the frequency range \( -5 \leq \omega \leq 5 \) : a) a plot of \( \left|c_{n}\right| \), b) a plot of \( |X(\omega)| \) and c) a plot of \( \angle c_{n}=\angle X(\omega) \). Comment on the significance of these plots in relation to amplitude and phase of harmonics