Home /
Expert Answers /
Mechanical Engineering /
problem-1-a-cantilever-beam-with-rectangular-cross-section-as-shown-in-fig-1-is-subjected-to-an-e-pa592
(Solved): Problem 1 A cantilever beam with rectangular cross section as shown in Fig. 1 is subjected to an e ...
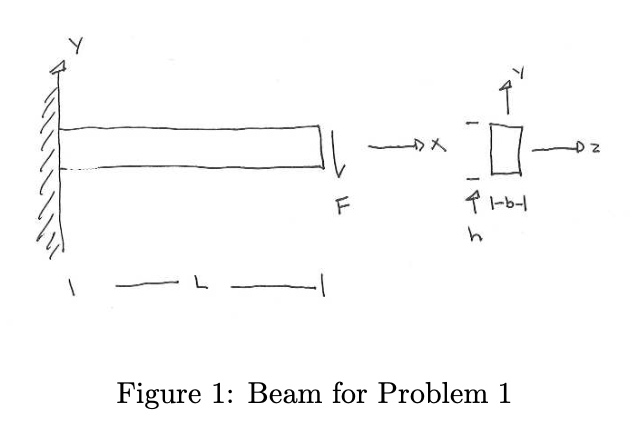
Problem 1 A cantilever beam with rectangular cross section as shown in Fig. 1 is subjected to an end loading at the free end. From solid mechanics the stress state at all points in the beam is described by where is the internal bending moment, is the internal shear load, is the moment of inertia about the z centroidal axis and a) (15 points) Show that the differential equations of equilibrium are satisfied at all points in the beam by the solid mechanics solution if body forces are negligible. b) (5 points) Check the equilibrium conditions on the boundary on all surfaces except the wall and determine whether the solid mechanics solution satisfies them. c)(5 points) Determine the shear, moment and axial stress resultants at the wall .
Figure 1: Beam for Problem 1
Expert Answer
a) To show that the differential equations of equilibrium are satisfied at all points in the beam by the solid mechanics solution, we need to verify that the equations of equilibrium are satisfied: (1) (2) (3)where F_x, F_y, and F_z are the body forces in the x, y, and z directions, respectively.We are given that Therefore, the only non-zero terms in the above equations are: Substituting these into Equation (1), we get: which is the equation of equilibrium for forces in the x direction. Similarly, we can verify the equilibrium conditions for forces in the y and z directions, which are automatically satisfied since the corresponding stresses are zero.