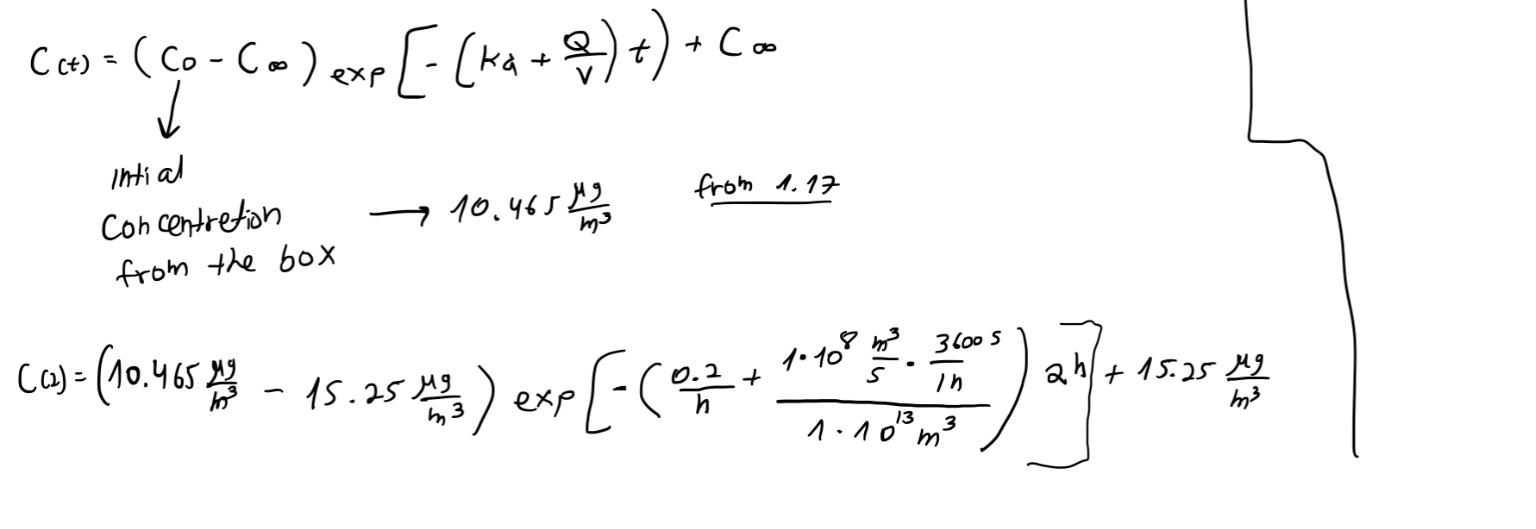(Solved): problem 1.18 can you show me the steps how to solve the equation with exp 1.17 Consider the air ov ...

problem 1.18

can you show me the steps how to solve the equation with exp

1.17 Consider the air over a city to be a box \( 100 \mathrm{~km} \) on a side that reaches up to an altitude of \( 1.0 \mathrm{~km} \). Clean air is blowing into the box along one of its sides with a speed of \( 4 \mathrm{~m} / \mathrm{s} \). Suppose an air pollutant with rate constant \( k=0.20 / \mathrm{hr} \) is emitted into the box at a total rate of \( 10.0 \mathrm{~kg} / \mathrm{s} \). Find the steady-state concentration if the air is assumed to be completely mixed. \( 1.18 \) If the windspeed in Problem \( 1.17 \) suddenly drops to \( 1 \mathrm{~m} / \mathrm{s} \), estimate the concentration of pollutants two hours later. \( \begin{aligned} C(t)=&\left(C_{0}-C_{\infty}\right) \exp \left[-\left(k_{a}+\frac{Q}{v}\right) t\right)+C_{\infty} \\ & \downarrow \\ & \text { intial } \\ & \text { Concentretion } \rightarrow 10.465 \frac{\mu g}{\mathrm{~m}^{3}} \text { from } 1.17 \\ & \text { from the box } \\ C(2)=&\left.\left(10.465 \frac{\mu g}{\mathrm{~m}^{3}}-15.25 \frac{\mu \mathrm{g}}{\mathrm{m}^{3}}\right) \exp \left[-\left(\frac{0.2}{\mathrm{~h}}+\frac{1 \cdot 10^{8} \frac{\mathrm{m}^{3}}{\mathrm{~s}} \cdot \frac{36005}{1 \mathrm{~h}}}{1 \cdot 10^{13} \mathrm{~m}^{3}}\right) 2 \mathrm{~h}\right]+15.25 \frac{\mu \mathrm{m}}{\mathrm{m}^{3}}\right] \end{aligned} \)