(Solved): Part 4: Thin Lens Equation This part of the lab will focus on quantitative measurements and testing ...

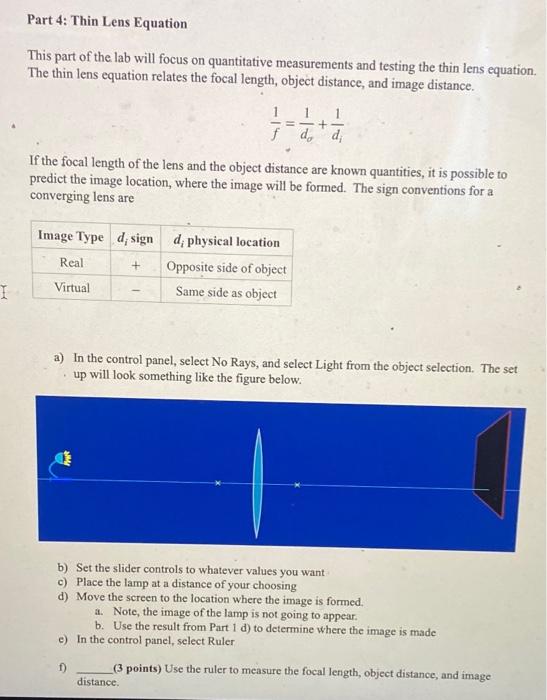
Part 4: Thin Lens Equation This part of the lab will focus on quantitative measurements and testing the thin lens equation. The thin lens equation relates the focal length, object distance, and image distance. \[ \frac{1}{f}=\frac{1}{d_{o}}+\frac{1}{d_{i}} \] If the focal length of the lens and the object distance are known quantities, it is possible to predict the image location, where the image will be formed. The sign conventions for a converging lens are a) In the control panel, select No Rays, and select Light from the object selection. The set up will look something like the figure below. b) Set the slider controls to whatever values you want c) Place the lamp at a distance of your choosing d) Move the screen to the location where the image is formed. a. Note, the image of the lamp is not going to appear. b. Use the result from Part \( 1 \mathrm{~d} \) ) to determine where the image is made e) In the control panel, select Ruler f) (3 points) Use the ruler to measure the focal length, object distance, and image distance. 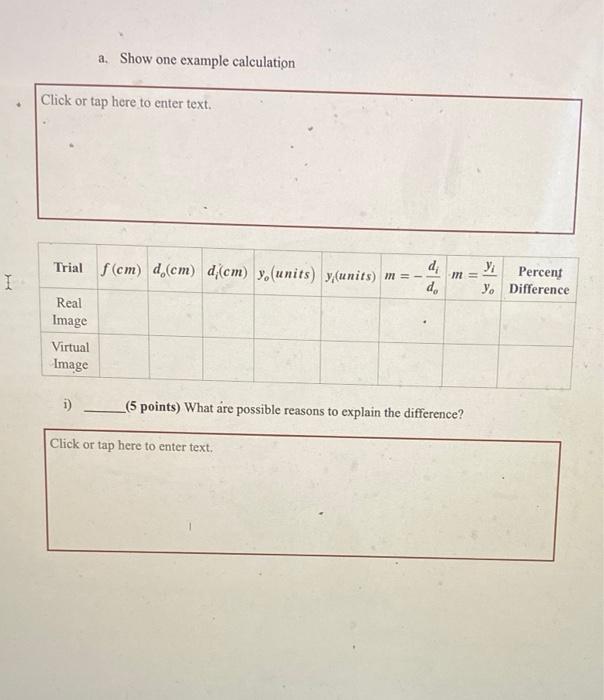a. Include screen shots of the 3 measurements Insert Screenshots Here g) Record the values in the Table provided h) (3 points) Change the slider settings and object distance. Then use the ruler to measure and record \( f, d_{e} \) and \( d_{i} \) until the table is completed i) (3 points) Use the thin lens equation to predict \( d_{i} \) for each trial a. Show one example calculation. j) (4 points) Perform a percent error calculation for each trial a. Show one example calculation k) (1 point) The screen was not able to be moved to the same side as the object. Even if you were able to move the screen to where the virtual image is located, would you see it on the screen? 1) In the control panel, select, Virtual Image and choose another Object. m) (2 points) Complete the table for virtual images n) (5 points) What are possible reasons to explain the error? This question should be answered with what did the user/investigator/student/experimentalist do while setting up with experiment or taking measurements that may be a cause for error? Part 5: Magnification The object height \( y_{o} \) is constant, but the image height \( y_{i} \) is not. Sometimes \( y_{i} \) is bigger. Other times \( y_{i} \) is smaller. The magnification of the object describes how much bigger or smaller the image is compared to the object. It is calculated with the equation \[ m \leqq \frac{y_{i}^{*}}{y_{o}}=-\frac{d_{i}}{d_{o}} \] a) In the control panel, select No Rays, Virtual Image, and Ruler. b) Set the slider controls to whatever values you want c) Place the object at a distance of your choosing d) Use the ruler to measure \( f_{,} d_{o} \), and \( d_{i} \) e) (5 points) The ruler cannot be rotated vertically to measure the object height. Create and describe a method to measure the height of the object on the screen (old question, the simulation now has a vertical ruler, enjoy the free 5 points). f) Complete the table below. g) (5 points) Calculate the magnification two ways for each trial a. Show one example calculation h) (3 points) Compare the magnification by calculating a percent difference for each a. Show one example calculation i) (5 points) What are possible reasons to explain the difference?