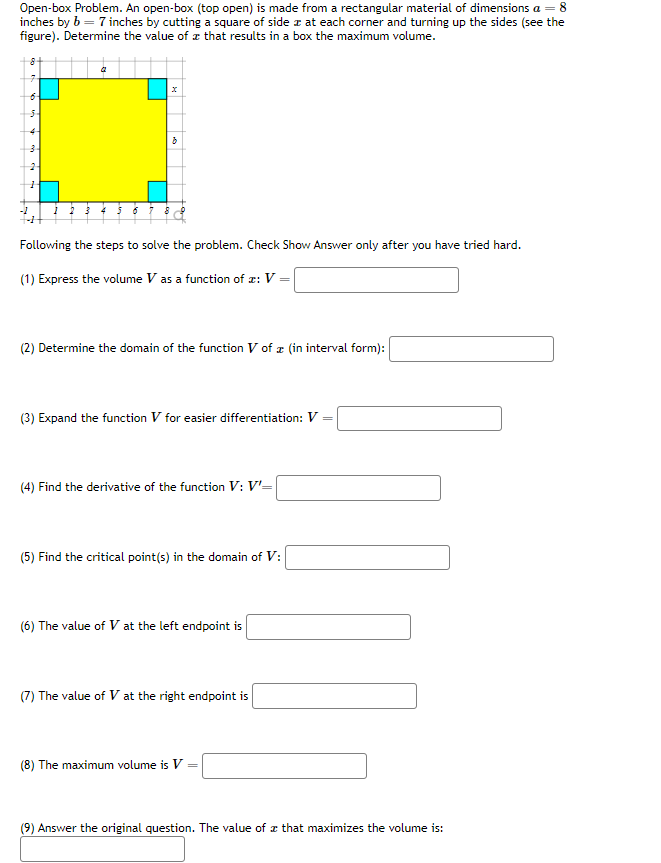
(Solved): Open-box Problem. An open-box (top open) is made from a rectangular material of dimensions a=8 inch ...

Open-box Problem. An open-box (top open) is made from a rectangular material of dimensions

inches by

inches by cutting a square of side

at each corner and turning up the sides (see the figure). Determine the value of

that results in a box the maximum volume. Following the steps to solve the problem. Check Show Answer only after you have tried hard. (1) Express the volume

as a function of

(2) Determine the domain of the function

of

(in interval form): (3) Expand the function

for easier differentiation:

(4) Find the derivative of the function

(5) Find the critical point(s) in the domain of

: (6) The value of

at the left endpoint is (7) The value of

at the right endpoint is (8) The maximum volume is

(9) Answer the original question. The value of

that maximizes the volume is: