(Solved):   Design a dopant diffusion process for a semiconductor that can yield a lateral sheet resis ...

 

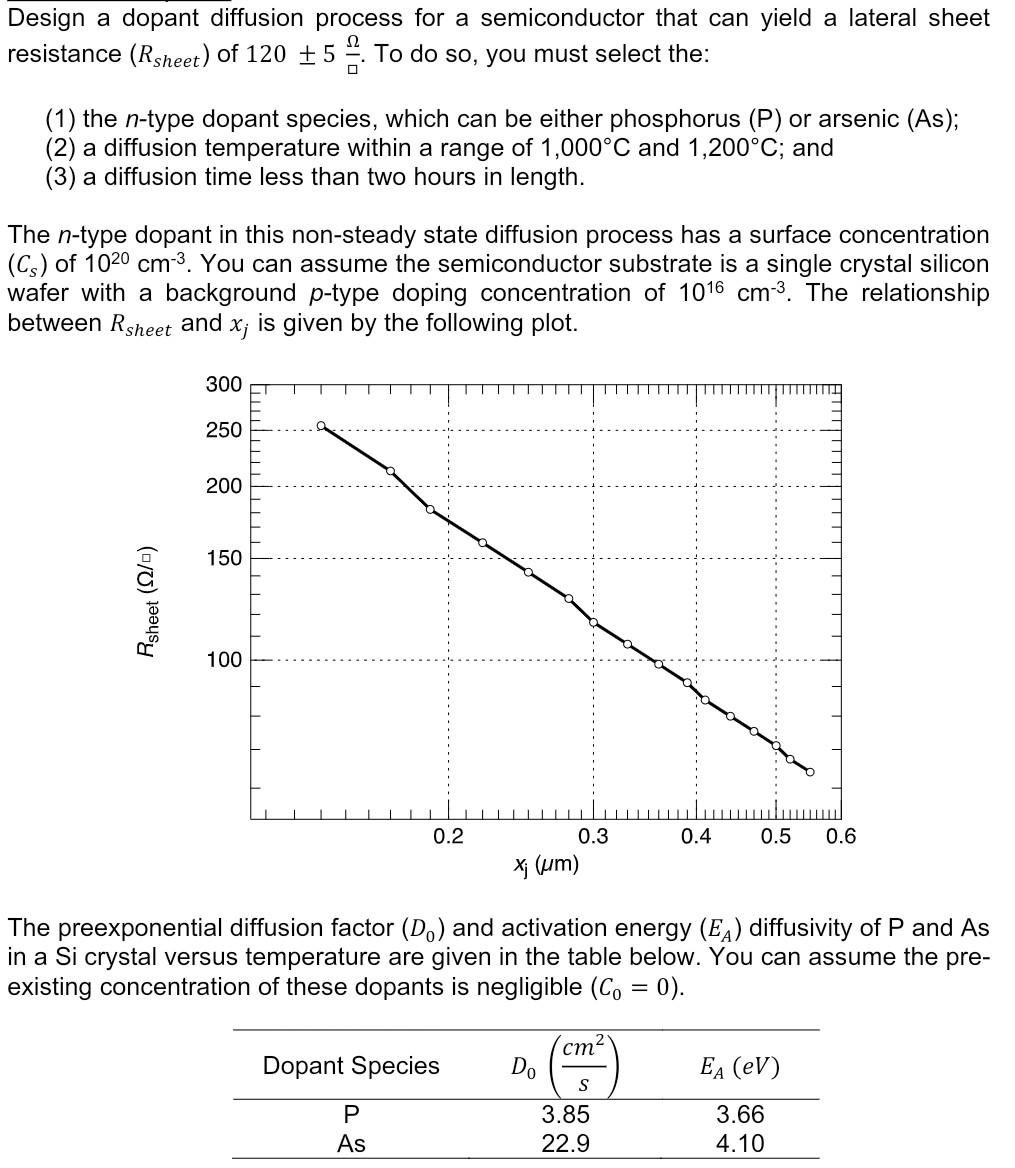
Design a dopant diffusion process for a semiconductor that can yield a lateral sheet resistance \( \left(R_{\text {sheet }}\right) \) of \( 120 \pm 5 \frac{\Omega}{\square} \). To do so, you must select the: (1) the \( n \)-type dopant species, which can be either phosphorus (P) or arsenic (As); (2) a diffusion temperature within a range of \( 1,000^{\circ} \mathrm{C} \) and \( 1,200^{\circ} \mathrm{C} \); and (3) a diffusion time less than two hours in length. The \( n \)-type dopant in this non-steady state diffusion process has a surface concentration \( \left(C_{s}\right) \) of \( 10^{20} \mathrm{~cm}^{-3} \). You can assume the semiconductor substrate is a single crystal silicon wafer with a background \( p \)-type doping concentration of \( 10^{16} \mathrm{~cm}^{-3} \). The relationship between \( R_{\text {sheet }} \) and \( x_{j} \) is given by the following plot. The preexponential diffusion factor \( \left(D_{0}\right) \) and activation energy \( \left(E_{A}\right) \) diffusivity of \( \mathrm{P} \) and \( \mathrm{As} \) in a Si crystal versus temperature are given in the table below. You can assume the preexisting concentration of these dopants is negligible \( \left(C_{0}=0\right) \).