(Solved): Learning Goal: To be able to find the center of gravity, the center of mass, and the centroid of a ...

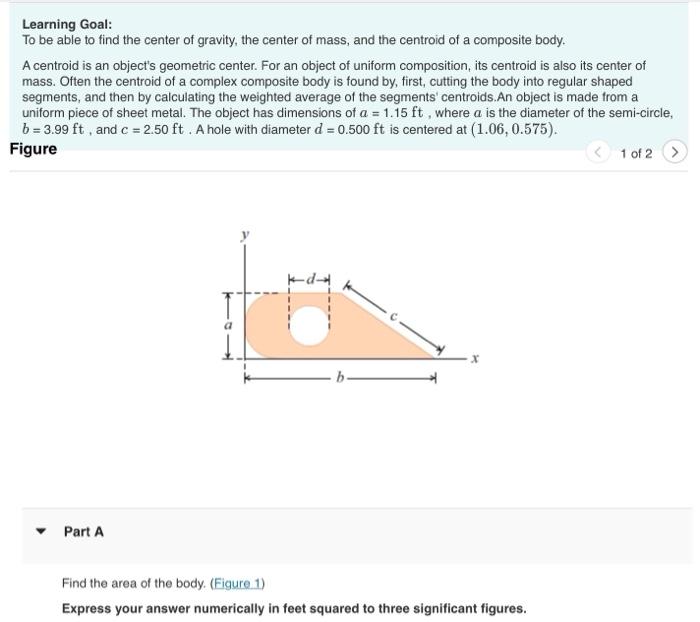
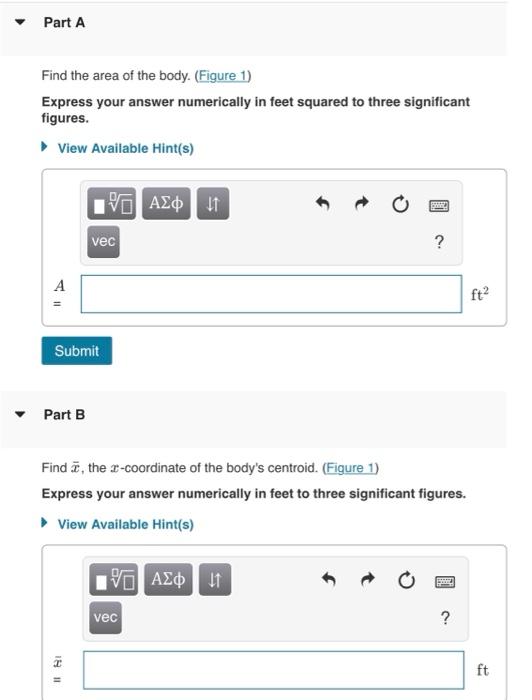
Learning Goal: To be able to find the center of gravity, the center of mass, and the centroid of a composite body. A centroid is an object's geometric center. For an object of uniform composition, its centroid is also its center of mass. Often the centroid of a complex composite body is found by, first, cutting the body into regular shaped segments, and then by calculating the weighted average of the segments' centroids.An object is made from a uniform piece of sheet metal. The object has dimensions of \( a=1.15 \mathrm{ft} \), where \( a \) is the diameter of the semi-circle, \( b=3.99 \mathrm{ft} \), and \( c=2.50 \mathrm{ft} \). A hole with diameter \( d=0.500 \mathrm{ft} \) is centered at \( (1.06,0.575) \). Figure 1 of 2 Part A Find the area of the body. (Figure 1) Express your answer numerically in feet squared to three significant figures. Find the area of the body. (Figure 1) Express your answer numerically in feet squared to three significant figures. vec ? A \[ = \] Part B Find \( \bar{x} \), the \( x \)-coordinate of the body's centroid. (Figure 1) Express your answer numerically in feet to three significant figures. 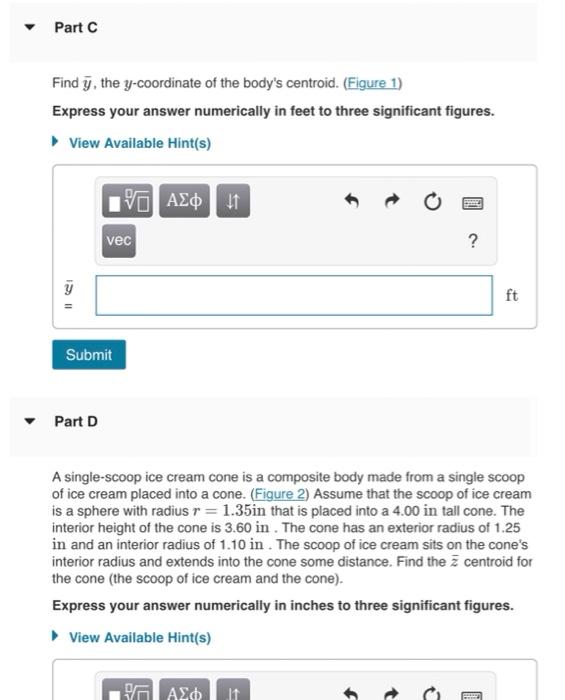Find \( \bar{y} \), the \( y \)-coordinate of the body's centroid. (Figure 1) Express your answer numerically in feet to three significant figures. \( \bar{y} \) \( = \) \( \mathrm{ft} \) Part D A single-scoop ice cream cone is a composite body made from a single scoop of ice cream placed into a cone. Assume that the scoop of ice cream is a sphere with radius \( r=1.35 \mathrm{in} \) that is placed into a \( 4.00 \) in tall cone. The interior height of the cone is \( 3.60 \mathrm{in} \). The cone has an exterior radius of \( 1.25 \) in and an interior radius of \( 1.10 \) in . The scoop of ice cream sits on the cone's interior radius and extends into the cone some distance. Find the \( \bar{z} \) centroid for the cone (the scoop of ice cream and the cone). Express your answer numerically in inches to three significant figures.