(Solved): Introduction A simple pendulum consists of a riass, called a bob, connected to the end of a ruspend ...

Introduction A simple pendulum consists of a riass, called a bob, connected to the end of a ruspended cord or string. When the bob is pulled to one side of its position of rest and thra released, it begins to wabrate In a simple harmonic motion. In geceral, a vibration is any back and forth motion that repeats itself Simiple harmonie motion oceun when there is a sestoring force that is equal to and ofpoute to a displacetnent. The restoring force, of course, ccmes from erayity acting cen the bob There are a number of factors that could affect the vibration of a ptedulum and this investigation in concersed with these factors. A vibrating pendolum cas be described by meanuring teveral variables. The exteat of duplacement from the rest position is calsed the anaplitude of the vibratice (C to \( \mathrm{A} \) - or \( \mathrm{B}- \) in Figure 6.I). A vibration that has the bob displaced a greater dietance from the reet position thus has a greater anplitude than a vibtation with less dieplacement. A complete vibration is called a cycle. A cycle is the movement from seme point (say the fur leA), to a maximum displacemsent in the other direction (lay the far niphti then back to the tame paint again (the far left). The period \( (T) \) is simply the time required to conslete cne cycle. For exanple; suppose 3 s it required for a bob to move through cone complete cycle, to complete the back-andforth motion from one point, then back to that point. The period of this vibration as 31 . Tbe uumber of cycles per second is called the frequency (D). For example, a tibrating bob that motes throegh -1 cycle in 1 is hat a frequency of 1 cycle per secoed. The length \( (L) \) of the geodulam is nesuared froen the point of suspension to the center of gravity of the bob. Ideally the mass of the bob ahould be concentrated at a ungle point. For a small homogensecut sphere, however, the distribited mass is affected by eravity almost as if the mass wete all located at the center of the sphere. 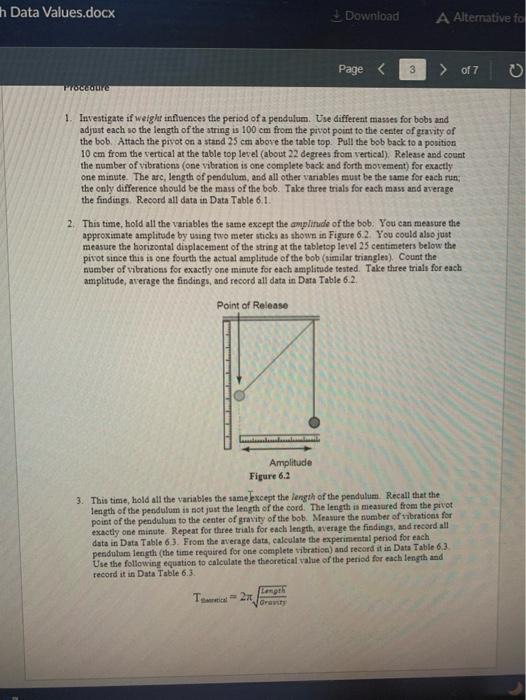For all practical purposes then, the lessth of the penduluen is the length of the card phat the racing ef the dob (aee Eigute 6.1) 1. Investigate if weight influences the period of a pendulnen. Use different masses for bobs and adjust each so the length of the atring is \( 100 \mathrm{~cm} \) from the pitot point to the center of gravity of the bob. Attach the pivot on a stand \( 25 \mathrm{~cm} \) above the table top. Pull the bob back to a position \( 10 \mathrm{~cm} \) from the vertical at the table top level (about 22 degrees from verticaf). Release and count the number of vibrations (one vibration is one complete back and forth movement) for exactly one minute. The arc, length of pendulum, and all other variables must be the same for each run; the only difference should be the mass of the bob. Take three trials for each mass and average the findings. Recotd all data in Data Table 6.1. 2. This time, hold all the variables the same except the amplinude of the bob. You can measure the approximate amplitude by using two meter sticks as shown in Figure \( 6.2 \). You could also just measure the horizontal displacement of the string at the tabletop level 25 centimeters below the pivot since this is one fourth the actual amplatude of the bob (similar triangles). Count the number of vibrations for exactly one minute for each amplitude tested. Take three trials for each amplitude, average the findings, and record all data in Data Table 6.2. 3. This time, hold all the variables the same except the length of the perdulumi Reeall that the length of the pendulum is not just the length of the cord. The length in measured from the prvot point of the pendulum to the center of gratity of the bob. Meavure the nomber of tibraticas for exactly one mainute. Repeat for three trials for each length, average the findings, and record all data in Data Table 6.3. From the average data, calculate the experimental period for each pendutum length (the timie required for one cemplete tibration) and record it in Data Table 6.3. Use the following equation to calculate the theoretical value of the period for each length and record it in Data Table 6.3. \[ \mathrm{T}_{\text {earutiat }}=2 \pi \sqrt{\frac{\text { Lengrt }}{\text { oravit }}} \] 1. According to your experimental results, what effect does the weight have on the period of a pendulum? 2. According to your experimental results, what effect does the amplitude have on the period of a pendulum? 3. According to your experimental results, what effect does the length have on the period of a pendulum? What is the proportional relationahip of the length and period of a pendulum? 4. Was the purpose of this lab accomplished? Why or why not? (Your answer to this question should be reasonable and make sense, showing thoughtful analysis and careful, thorough thinking.)