Home /
Expert Answers /
Calculus /
if-f-and-g-are-the-functions-whose-graphs-are-shown-let-u-x-f-g-x-v-x-g-f-x-and-w-x-g-g-x-pa616
(Solved): If f and g are the functions whose graphs are shown, let u(x)=f(g(x)),v(x)=g(f(x)), and w(x)=g(g(x) ...
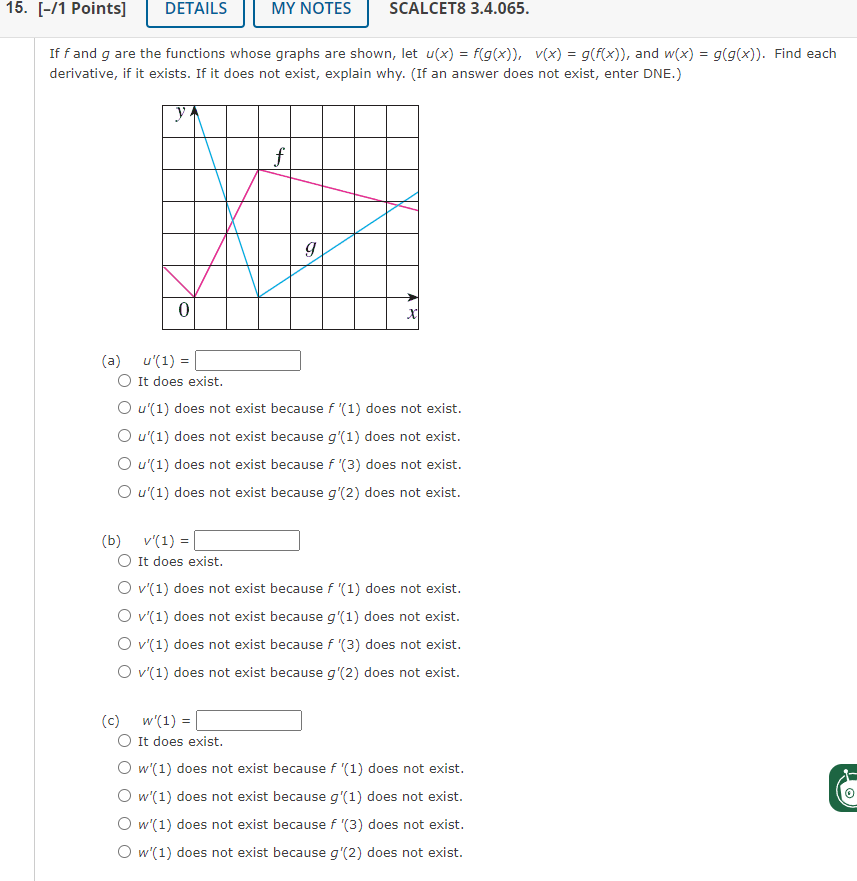
If
fand
gare the functions whose graphs are shown, let
u(x)=f(g(x)),v(x)=g(f(x)), and
w(x)=g(g(x)). Find each derivative, if it exists. If it does not exist, explain why. (If an answer does not exist, enter DNE.) (a)
u^(')(1)=It does exist.
u^(')(1)does not exist because
f^(')(1)does not exist.
u^(')(1)does not exist because
g^(')(1)does not exist.
u^(')(1)does not exist because
f^(')(3)does not exist.
u^(')(1)does not exist because
g^(')(2)does not exist. (b)
v^(')(1)=It does exist.
v^(')(1)does not exist because
f^(')(1)does not exist.
V^(')(1)does not exist because
g^(')(1)does not exist.
v^(')(1)does not exist because
f^(')(3)does not exist.
v^(')(1)does not exist because
g^(')(2)does not exist. (c)
w^(')(1)=It does exist.
w^(')(1)does not exist because
f^(')(1)does not exist.
w^(')(1)does not exist because
g^(')(1)does not exist.
w^(')(1)does not exist because
f^(')(3)does not exist.
w^(')(1)does not exist because
g^(')(2)does not exist.