Home /
Expert Answers /
Algebra /
if-b-is-the-standard-basis-of-the-space-p-3-of-polynomials-then-let-b-1-tt-2-t-3-use-coor-pa584
(Solved): If B is the standard basis of the space P_(3) of polynomials, then let B={1,tt^(2),t^(3)}. Use coor ...
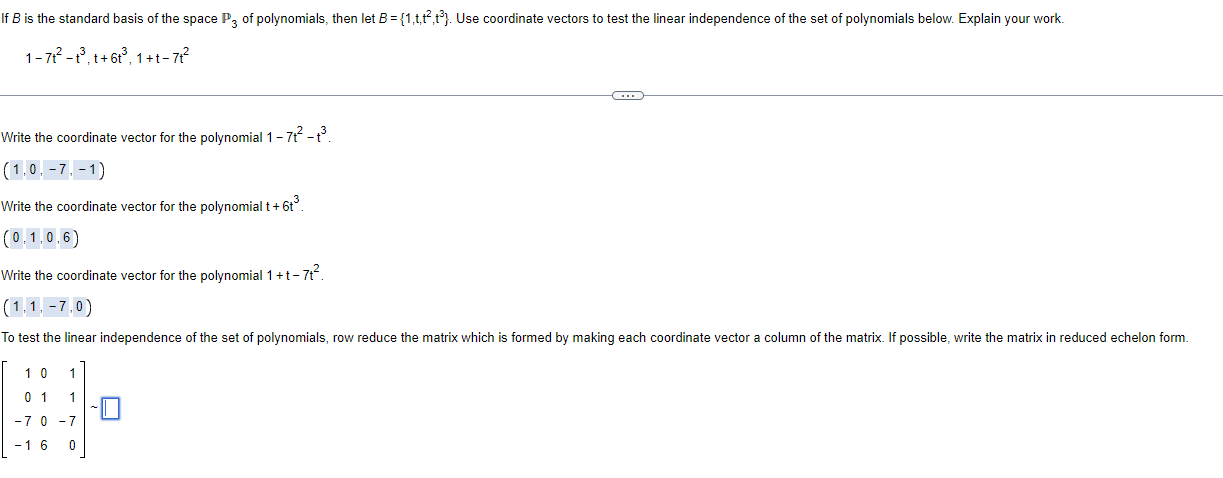
If
Bis the standard basis of the space
P_(3)of polynomials, then let
B={1,tt^(2),t^(3)}. Use coordinate vectors to test the linear independence of the set of polynomials below. Explain your work.
1-7t^(2)-t^(3),t+6t^(3),1+t-7t^(2)Write the coordinate vector for the polynomial
1-7t^(2)-t^(3).
(1,0,-7,-1)Write the coordinate vector for the polynomial
t+6t^(3).
(0,1,0,6)Write the coordinate vector for the polynomial
1+t-7t^(2).
(1,1,-7,0)To test the linear independence of the set of polynomials, row reduce the matrix which is formed by making each coordinate vector a column of the matrix. If possible, write the matrix in reduced echelon form.
[[1,0,1],[0,1,1],[-7,0,-7],[-1,6,0]]∼