Home /
Expert Answers /
Calculus /
i-really-need-this-fvaluate-the-iterated-integral-by-converting-to-polar-coordinates-int-0-6-pa714
(Solved): i really need this Fvaluate the iterated integral by converting to polar coordinates. \[ \int_{0}^{6 ...
i really need this
![Fvaluate the iterated integral by converting to polar coordinates.
\[
\int_{0}^{6} \int_{0}^{\sqrt{6 x-x^{2}}} x y d y d x
\]](https://media.cheggcdn.com/study/bae/bae7ef14-1544-4411-8197-05d3e898b8dc/image)
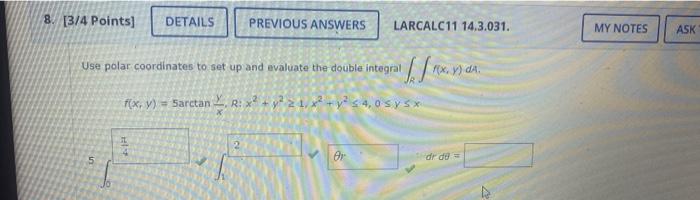
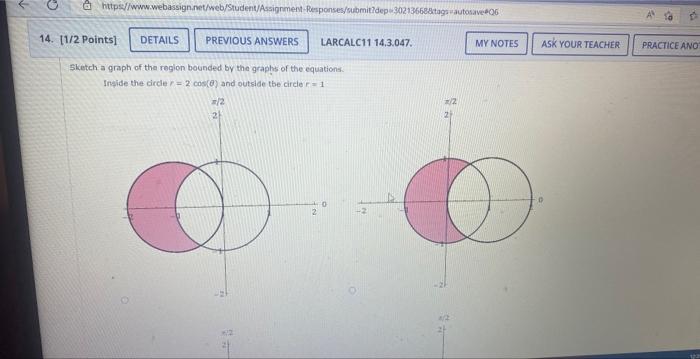
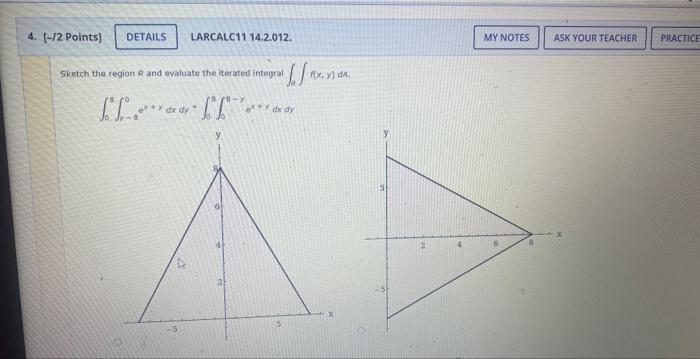
Fvaluate the iterated integral by converting to polar coordinates. \[ \int_{0}^{6} \int_{0}^{\sqrt{6 x-x^{2}}} x y d y d x \]
Use polar coordinates to set up and evaluate the double integral \( \int_{R} \int f(x, y) d A \). \[ f(x, y)=5 \arctan \frac{y}{x}, R: x^{2}+y^{2} \geq 1, x^{2}+y^{2} \leq 4,0 \leq y \leq x \] \[ d r d t= \]
Sketch a graph of the region bounded by the graphs of the equations: Inside the circle \( r=2 \cos (\theta) \) and outside the circle \( r=1 \)
Sketch the region \( R \) and evaluate the iterated integral \( \int_{R} \int f(x, y) d A \). \[ \int_{0}^{8} \int_{y-a}^{0} e^{x+y} d x d y+\int_{0}^{8} \int_{0}^{8-y} e^{x+y} d x d y \]
Expert Answer
6. Let the given integral is I=?06?06x?x2xydydx hence we can see that integration region is bounded by