(Solved): help soon please Compute each matrix sum or product if it is defined. If an expression is undefined, ...

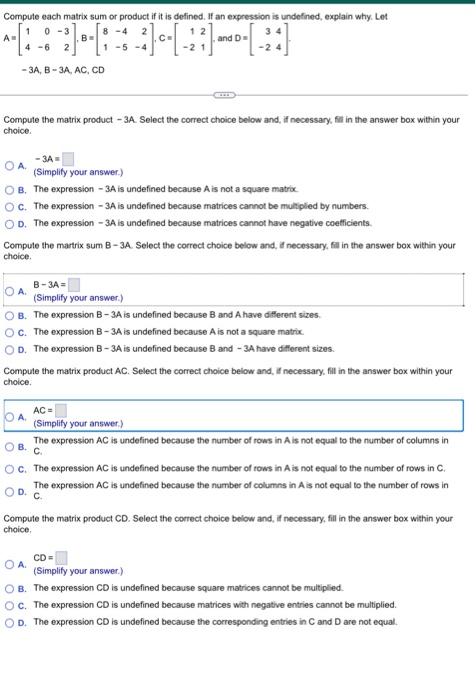
Compute each matrix sum or product if it is defined. If an expression is undefined, explain why. Let \[ \begin{aligned} A &=\left[\begin{array}{rrr} 1 & 0 & -3 \\ 4 & -6 & 2 \end{array}\right], B=\left[\begin{array}{rrr} 8 & -4 & 2 \\ 1 & -5 & -4 \end{array}\right], C=\left[\begin{array}{rr} 1 & 2 \\ -2 & 1 \end{array}\right] \text {, and } D=\left[\begin{array}{rr} 3 & 4 \\ -2 & 4 \end{array}\right] \\ &-3 A, B-3 A, A C, C D \end{aligned} \] Compute the matrix product - 3A. Select the correct choice below and, if necessary, fili in the answer box within your choice. A. \( -3 A= \) (Simplify your answer.) B. The expression - \( 3 \mathrm{~A} \) is undefined because \( \mathrm{A} \) is not a square matrix. C. The expression \( -3 \mathrm{~A} \) is undefined because matrices cannot be mulfipled by numbers. D. The expression \( -3 \mathrm{~A} \) is undefined because matrices cannot have negative coefficients. Compute the martrix sum B - 3A. Select the correct choice below and, it necessary, fill in the answer box within your choice. A. \( \mathrm{B}-3 \mathrm{~A}= \) (Simplify your answer.) B. The expression \( B-3 A \) is undefined because \( B \) and \( A \) have different sizes. C. The expression \( \mathrm{B}-3 \mathrm{~A} \) is undefined because \( \mathrm{A} \) is not a square matrix. D. The expression \( B-3 A \) is undefined because \( B \) and \( -3 A \) have different sizes. Compute the matrix product AC. Select the correct choice below and, If necessary, fill in the answer box within your choice. A. \( \mathrm{AC}= \) (Simplify your answer.) B. The expression \( \mathrm{AC} \) is undefined because the number of rows in \( \mathrm{A} \) is not equal to the number of columns in B. C. c. The expression \( A C \) is undefined because the number of rows in \( A \) is not equal to the number of rows in \( C \). D. The expression \( A C \) is undefined because the number of columns in \( A \) is not equal to the number of rows in C. Compute the matrix product CD. Select the correct choice below and, if necessary, fill in the answer box within your choice. A. \( C D= \) A. (Simplify your answer.)