(Solved): he toggle mechanism shown (Figure below) moves to a final \( \theta=30^{\circ} \). What will be th ...

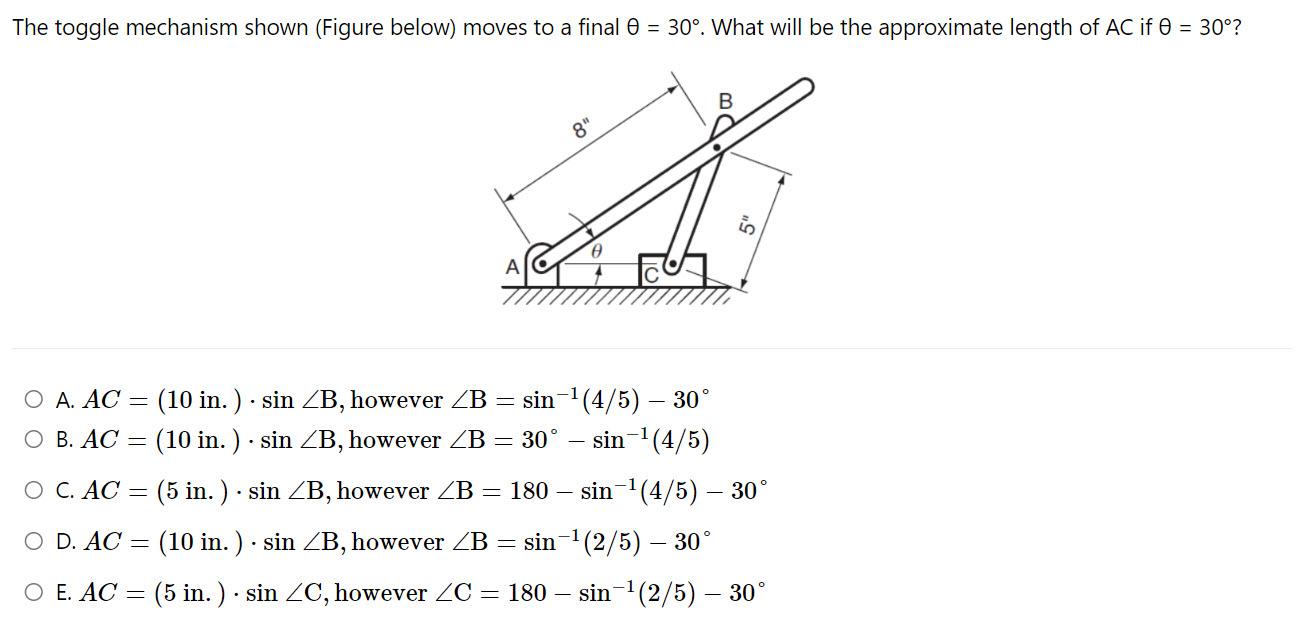
he toggle mechanism shown (Figure below) moves to a final \( \theta=30^{\circ} \). What will be the approximate length of \( A C \) if \( \theta=30^{\circ} \) ? A. \( A C=(10 \) in. \( ) \cdot \sin \angle \mathrm{B} \), however \( \angle \mathrm{B}=\sin ^{-1}(4 / 5)-30^{\circ} \) B. \( A C=(10 \) in. \( ) \cdot \sin \angle \mathrm{B} \), however \( \angle \mathrm{B}=30^{\circ}-\sin ^{-1}(4 / 5) \) C. \( A C=(5 \) in. \( ) \cdot \sin \angle \mathrm{B} \), however \( \angle \mathrm{B}=180-\sin ^{-1}(4 / 5)-30^{\circ} \) D. \( A C=(10 \) in. \( ) \cdot \sin \angle \mathrm{B} \), however \( \angle \mathrm{B}=\sin ^{-1}(2 / 5)-30^{\circ} \) E. \( A C=(5 \) in. \( ) \cdot \sin \angle \mathrm{C} \), however \( \angle \mathrm{C}=180-\sin ^{-1}(2 / 5)-30^{\circ} \)