(Solved): he home run percentage is the number of home runs per 100 times at bat. A random sample of 43 profe ...

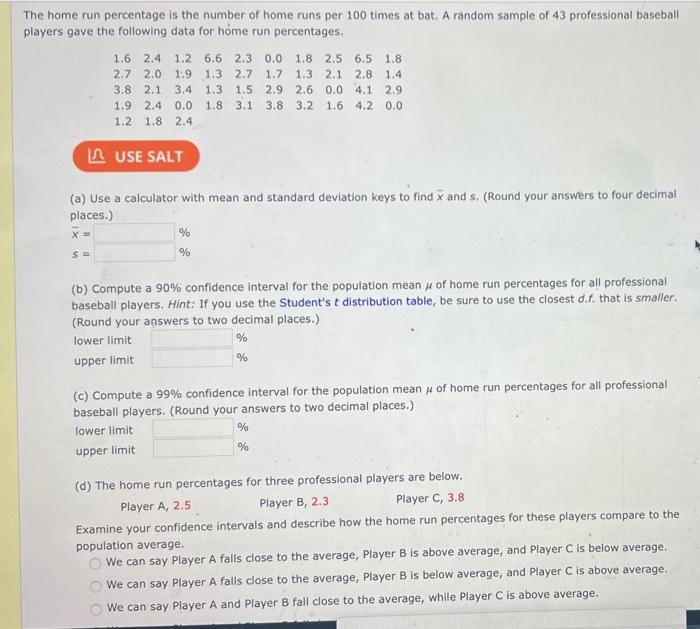
he home run percentage is the number of home runs per 100 times at bat. A random sample of 43 professional baseball layers gave the following data for hóme run percentages. \( \begin{array}{llllllllll}1.6 & 2.4 & 1.2 & 6.6 & 2.3 & 0.0 & 1.8 & 2.5 & 6.5 & 1.8 \\ 2.7 & 2.0 & 1.9 & 1.3 & 2.7 & 1.7 & 1.3 & 2.1 & 2.8 & 1.4 \\ 3.8 & 2.1 & 3.4 & 1.3 & 1.5 & 2.9 & 2.6 & 0.0 & 4.1 & 2.9 \\ 1.9 & 2.4 & 0.0 & 1.8 & 3.1 & 3.8 & 3.2 & 1.6 & 4.2 & 0.0 \\ 1.2 & 1.8 & 2.4 & & & & & & & \end{array} \) (a) Use a calculator with mean and standard deviation keys to find \( \bar{x} \) and \( s \). (Round your answers to four decimal places.) \( \begin{array}{ll}\bar{x}= & \% \\ s= & \%\end{array} \) (b) Compute a \( 90 \% \) confidence interval for the population mean \( \mu \) of home run percentages for all professional baseball players. Hint: If you use the Student's \( t \) distribution table, be sure to use the closest d.f. that is smaller. (Round your answers to two decimal places.) lower limit- upper limit (c) Compute a \( 99 \% \) confidence interval for the population mean \( \mu \) of home run percentages for all professional baseball players. (Round your answers to two decimal places.) lower limit \( \% \)