(Solved): Gravel is falling on a conical pile at the rate of \( 32 \frac{\mathrm{ft}^{3}}{\mathrm{~min}} \). ...

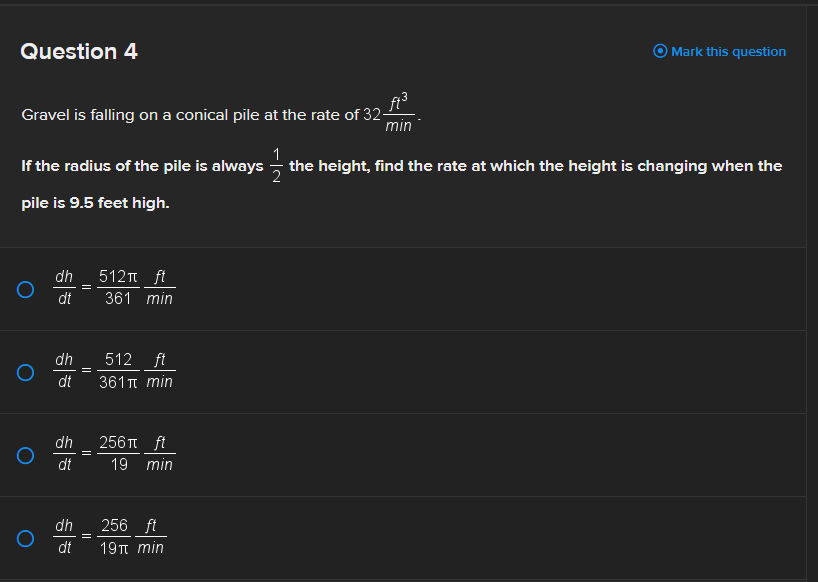
Gravel is falling on a conical pile at the rate of \( 32 \frac{\mathrm{ft}^{3}}{\mathrm{~min}} \). If the radius of the pile is always \( \frac{1}{2} \) the height, find the rate at which the height is changing when the pile is \( 9.5 \) feet high. \( \frac{d h}{d t}=\frac{512 \pi}{361} \frac{f t}{\min } \) \( \frac{d h}{d t}=\frac{512}{361 \pi} \frac{f t}{\min } \) \( \frac{d h}{d t}=\frac{256 \pi}{19} \frac{f t}{\min } \) \( \frac{d h}{d t}=\frac{256}{19 \pi} \frac{f t}{\min } \)