(Solved): Free-body diagram Part of riding a bicycle involves leaning at the correct angle when making a ...

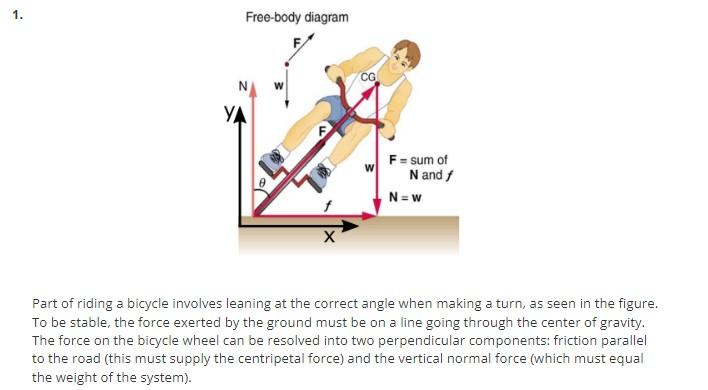
Free-body diagram Part of riding a bicycle involves leaning at the correct angle when making a turn, as seen in the figure. To be stable, the force exerted by the ground must be on a line going through the center of gravity. The force on the bicycle wheel can be resolved into two perpendicular components: friction parallel to the road (this must supply the centripetal force) and the vertical normal force (which must equal the weight of the system). (a) Express friction and normal force in terms of \( F \) and \( \theta \). \[ N= \] \( \mathrm{F} \) Fsin \( \theta \) \( F \cos \theta \) \( -\mathrm{F} \sin \theta \) \( -\mathrm{F} \cos \theta \) (1) \( f= \) F \( F \sin \theta \) \( F \cos \theta \) \( -\mathrm{F} \sin \theta \) \( -\mathrm{F} \cos \theta \) (b) Write Newton's second law for the horizontal and vertical directions. Take rightward to be the \( +x- \) direction and vertically upward to be +y-direction. Write your equations in terms of the normal force \( N \), friction \( f, \operatorname{mass} m \), and \( g \). \[ \begin{array}{ll} F_{\text {net }, x}=1 & =m v^{2} / r(3) \\ F_{\text {net }, V}=1 & ]=0 \text { (4) } \end{array} \] (c) Find an equation relating \( \tan (\theta) \) with the speed of the bicycle \( v \), radius \( r \), and acceleration due to gravity, g. Hint: equate the vector decomposition of \( F(1) \) and (2) to your results from part (b) - (3) and (4). To type your equations, you can enter Greek letters by selecting the MathType popup button (red radical) in the answer box. For Greek letters, press the right-facing arrow next to the alpha (a) symbol. \[ \tan (\theta)= \] (d) Based on your answer for \( (\mathrm{c}) \), if the bicycle is vertical \( \left(\theta=0^{\circ}\right. \) ), will it be able to traverse the curve while maintaining balance? yes no Why? (e) Calculate \( \theta \) for a \( 10.5 \mathrm{~m} / \mathrm{s} \) turn of radius \( 28.5 \mathrm{~m} \).