(Solved): For the simply supported beam subjected to the loading shown, derive equation ...

???????

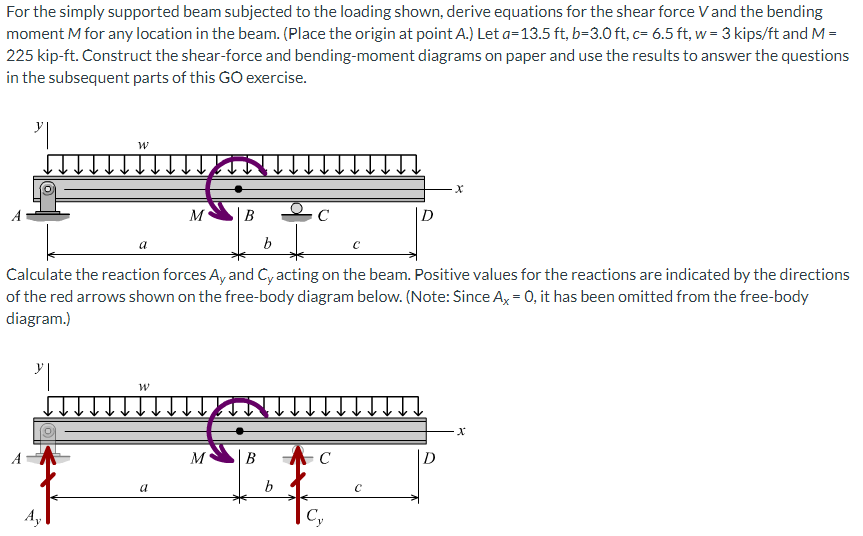
For the simply supported beam subjected to the loading shown, derive equations for the shear force \( V \) and the bending moment \( M \) for any location in the beam. (Place the origin at point \( A \).) Let \( a=13.5 \mathrm{ft}, b=3.0 \mathrm{ft}, c=6.5 \mathrm{ft}, w=3 \mathrm{kips} / \mathrm{ft} \) and \( M= \) 225 kip-ft. Construct the shear-force and bending-moment diagrams on paper and use the results to answer the questions in the subsequent parts of this \( \mathrm{GO} \) exercise. Calculate the reaction forces \( A_{y} \) and \( C_{y} \) acting on the beam. Positive values for the reactions are indicated by the directions of the red arrows shown on the free-body diagram below. 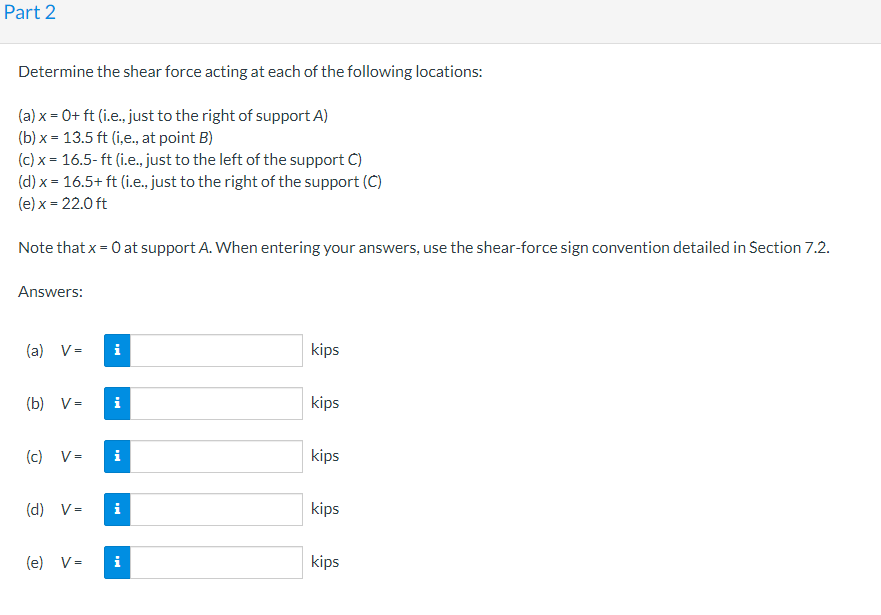(Note: Since \( A_{x}=0 \), it has been omitted from the free-body diagram.) Determine the shear force acting at each of the following locations: (a) \( x=0+f t \) (i.e., just to the right of support A) (b) \( x=13.5 \mathrm{ft} \) (i,e., at point \( B \) ) (c) \( x=16.5-f t \) (i.e., just to the left of the support C) (d) \( x=16.5+ \) ft (i.e., just to the right of the support (C) (e) \( x=22.0 \mathrm{ft} \) Note that \( x=0 \) at support \( A \). When entering your answers, use the shear-force sign convention detailed in Section 7.2. 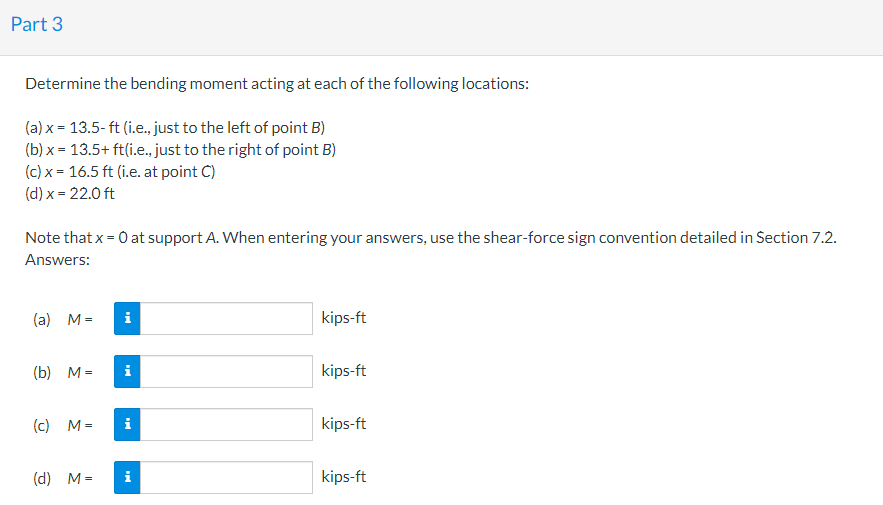Answers: (a) \( V= \) kips (b) \( \quad V= \) kips (c) \( V= \) kips (d) \( V= \) kips (e) \( V= \) kips Determine the bending moment acting at each of the following locations: (a) \( x=13.5-f t \) (i.e., just to the left of point \( B \) ) (b) \( x=13.5+ \) ft(i.e., just to the right of point \( B \) ) (c) \( x=16.5 \mathrm{ft} \) (i.e. at point C) (d) \( x=22.0 \mathrm{ft} \) Note that \( x=0 \) at support \( A \). When entering your answers, use the shear-force sign convention detailed in Section 7.2. Answers: (a) \( M= \) kips-ft (b) \( M= \) kips-ft (c) \( M= \) kips-ft (d) \( M= \) kips-ft Use your shear-force and bending-moment diagrams to determine the maximum positive bending moment, \( M_{\max } \), pos, the maximum negative bending moment, \( M_{\max } \) neg, and their respective locations, \( x_{\max } \), pos and \( x_{\max } \), neg. When entering your answers for the maximum bending moments, use the shear-force and bending-moment sign conventions detailed in Section 7.2. The maximum negative bending moment is the negative moment with the largest absolute value. Enter the maximum negative bending moment as a negative value. Answers: \( \begin{array}{llll}M_{\max , \text { pos }}= & \operatorname{kips}-\mathrm{ft} \quad x_{\max , \text { pos }}= & \mathrm{ft} \\ M_{\max , \mathrm{neg}}= & \text { kips-ft } \quad x_{\max , \mathrm{neg}}= & \mathrm{ft}\end{array} \)