(Solved): For the beam and loading shown, use discontinuity functions to compute (a) the slope of the beam at ...

For the beam and loading shown, use discontinuity functions to compute (a) the slope of the beam at \( B \). (b) the deflection of the beam at \( \mathrm{B} \). Assume a constant value of El \( -130,000 \mathrm{kN} \cdot \mathrm{m}^{2} \) for the beam Let \( w_{A}-20 \mathrm{kN} / \mathrm{m}_{1}, w_{B}-41 \mathrm{kN} / \mathrm{m}, \mathrm{L}=4,75 \mathrm{~m} \). Calculate the reaction force \( A_{y} \) and the teaction moment, \( M_{L} \) acting on the beam. Positive values for the reactions are indicated by the directions of the red arrows shown on the free body diagram below. (Note: Since \( A_{x}=0 \), it has been omitted from the free: body diagram) Answers: \( \begin{array}{ll}A_{x}= & k N \\ M_{A}= & k N-m\end{array} \) For this loading, select the correct moment expression \( M(x) \) from those listed below, where each expression is based on discontinuity functions. Answer: (b) \( M(x)=M_{1}(x-0 m)^{0}+A_{p}(x-0 m)^{1}+\frac{w_{A}}{2}(x-0 m)^{2}+\frac{w_{n}-w_{A}}{6(4.75 m)}(x-0 m)^{3}-\frac{w_{A}}{2}(x-4.75 m)^{2}-\frac{w_{n}-w_{1}}{6(4.75 m)} \) (e) \( M(x)=-\frac{w_{A}}{2}(x-0 m)^{2}-\frac{w_{B}-w_{A}}{6(4.75 m)}(x-0 m)^{3}+\frac{w_{A}}{2}(x-4.75 m)^{2}+\frac{w_{B}-w_{A}}{6(4.75 m)}(x-4.75 m)^{3}+\frac{w_{B}-w_{A}}{2}\langle x- \) (c) \( M(x)=M_{A}(x-0 m)^{\prime}+A_{2}(x-0 m)^{\prime}+\frac{w_{A}}{2}(x-0 m)^{2}+\frac{w_{n}-w_{A}}{6(4.75 m)}(x-0 m)^{3}-\frac{w_{A}}{2}(x-4.75 m)^{2}-\frac{w_{n}-w_{A}}{6(4.75 m)}(x) \) \( M(x)=\frac{w_{A}}{2}(x-0 m)^{2}+\frac{w_{n}-w_{A}}{6(4.75 m)}(x-0 m)^{3}-\frac{w_{A}}{2}(x-4.75 m)^{2}-\frac{w_{n}-w_{A}}{6(4.75 m)}(x-4.75 m)^{2}-\frac{w_{n}-w_{A}}{2}(x-4.75 \) (d) \( M(x)=M_{1}(x-0 m)^{-1}+\lambda,\langle x-0 m)^{0}-\frac{w_{A}}{2}(x-0 m)^{\prime}-\frac{w_{n}-w_{A}}{6(4.75 m)}(x-0 m)^{2}+\frac{w_{A}}{2}(x-4.75 m)^{1}+\frac{w_{n}-w_{1}}{6(4.75 m)}(x) \) (3) 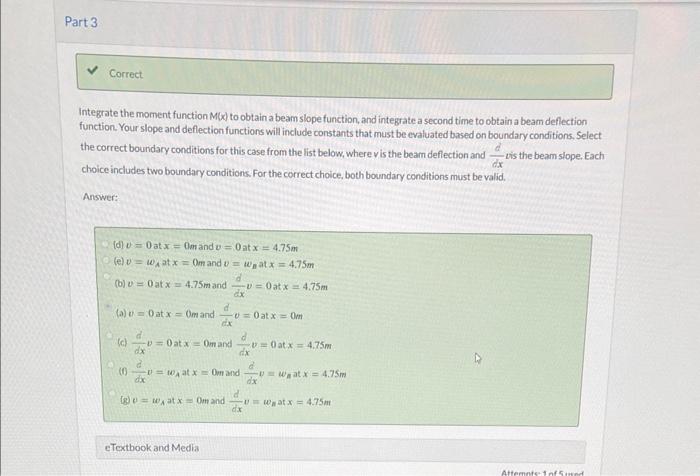Integrate the moment function \( M(x) \) to obtain a beam slope function, and integrate a second time to obtain a beam deflection function. Your slope and deflection functions will include constants that must be evaluated based on boundary conditions, Select. the correct boundary conditions for this case from the list below, where vis the beam deflection and \( \frac{d}{d x} v \) is the beam slope. Each choice includes two boundary conditions. For the correct choice, both boundary conditions must be valid. Answer: (d) \( v=0 \) at \( x=0 \mathrm{~m} \) and \( v=0 \) at \( x=4.75 \mathrm{~m} \) (e) \( v=w_{A} \) at \( x=0 \mathrm{~m} \) and \( v=w_{n} \) at \( x=4.75 \mathrm{~m} \) (b) \( v=0 \) at \( x=4.75 \mathrm{~m} \) and \( \frac{d}{d x} v=0 a t x=4.75 \mathrm{~m} \) (a) \( v=0 \) at \( x=0 \mathrm{~m} \) and \( \frac{d}{d x} v=0 \) at \( x=0 \mathrm{~m} \) (c) \( \frac{d}{d x} v=0 \mathrm{at} x=0 \mathrm{~m} \) and \( \frac{d}{d x} v=0 \mathrm{at} x=4.75 \mathrm{~m} \) (0) \( \frac{d}{d x} \nu=w_{A} \) at \( x=0 m \) and \( \frac{d}{d x} \nu=w_{n} \) at \( x=4.75 m \) (g) \( v=w_{n} \) at \( x=0 \) mand \( \frac{d}{d x} v=w_{n} \) at \( x=4.75 m \) 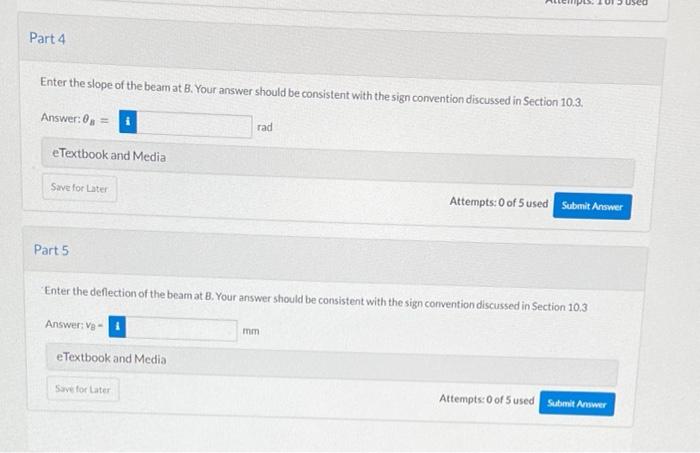Enter the slope of the beam at B. Your answer should be consistent with the sign convention discussed in Section 10.3. Answer: \( \theta_{n}= \) rad Attempts: 0 of 5 used \( \operatorname{Part} 5 \) Enter the deflection of the beam at B, Your answer should be consistent with the sign convention discussed in Section \( 10.3 \) Answer: \( v_{8}= \) \( \mathrm{mm} \) eTextbook and Media Attempts: 0 of 5 used