(Solved): For a radionuclide as used in nuclear imaging the number of radioactive nuclei decreases exponentia ...

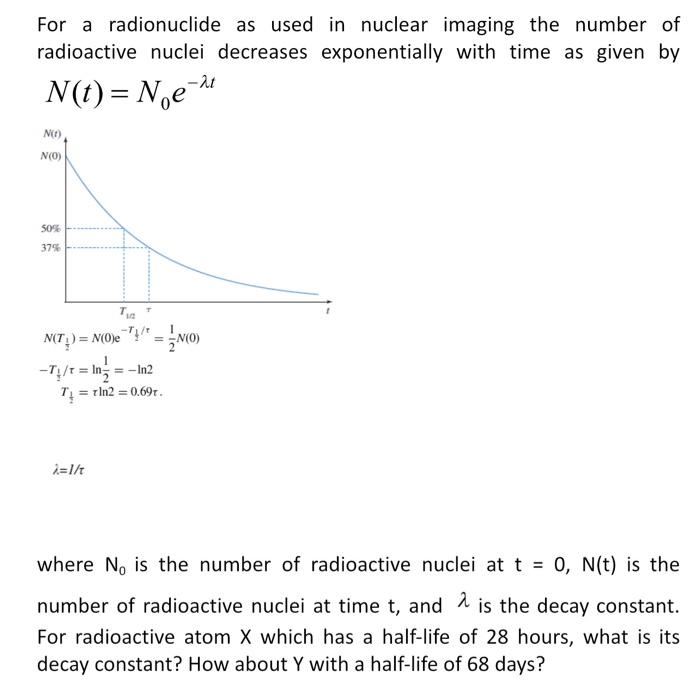
For a radionuclide as used in nuclear imaging the number of radioactive nuclei decreases exponentially with time as given by \( N(t)=N_{0} e^{-\lambda t} \) \[ \begin{aligned} N\left(T_{\frac{1}{2}}\right) &=N(0) \mathrm{e}^{-T_{\mathrm{t}}^{2} / \tau}=\frac{1}{2} N(0) \\ -T_{\frac{1}{4} / \tau} &=\ln \frac{1}{2}=-\ln 2 \\ T_{\frac{1}{2}} &=\tau \ln 2=0.69 \mathrm{r} . \end{aligned} \] \( i=1 / \tau \) where \( N_{0} \) is the number of radioactive nuclei at \( t=0, N(t) \) is the number of radioactive nuclei at time \( t \), and \( \lambda \) is the decay constant. For radioactive atom \( X \) which has a half-life of 28 hours, what is its decay constant? How about \( Y \) with a half-life of 68 days?