(Solved): FIRST sets calculation rules: 1. FIRST \( (x)=\{x\} \) if \( \mathrm{x} \) is a terminal. II. FIRST ...

FIRST sets calculation rules: 1. FIRST \( (x)=\{x\} \) if \( \mathrm{x} \) is a terminal. II. FIRST \( (\varepsilon)=\{\varepsilon\} \) III. If \( A \longrightarrow X \alpha \), then add FIRST \( (X)-\{\varepsilon\} \) to FIRST \( (A) \). IV. If \( A \longrightarrow A_{1} A_{2} A_{3} \ldots A_{i} A_{i+1} \ldots A_{k} \) and \( \varepsilon \in F I R S T\left(A_{1}\right) \) and \( \varepsilon \in F I R S T\left(A_{2}\right) \) and \( \ldots \) \( \varepsilon \in F I R S T\left(A_{i}\right) \) then add FIRST \( \left(A_{i+1}\right)-\{\varepsilon\} \) to FIRST \( (A) \) V. If \( A \longrightarrow A_{1} A_{2} A_{3} \ldots A_{k} \) and \( \varepsilon \in F I R S T\left(A_{1}\right) \) and \( \varepsilon \in F I R S T\left(A_{2}\right) \) and \( \ldots \varepsilon \in F I R S T\left(A_{k}\right) \) then add \( \varepsilon \) to \( F I R S T(A) \) FOLLOW sets calculation rules: 1. If \( S \) is the starting symbol of the grammar then add \( \$ \) (or EOF) to FOLLOW \( (S) \) II. If \( A \longrightarrow \alpha B \) then add \( F O L L O W(A) \) to FOLLOW \( (B) \) III. if \( A \longrightarrow \alpha B A_{1} A_{2} \ldots A_{k} \) and \( \varepsilon \in F I R S T\left(A_{1}\right) \) and \( \varepsilon \in F I R S T\left(A_{2}\right) \) and \( \ldots \varepsilon \in F I R S T\left(A_{k}\right) \) then add \( F O L L O W(A) \) to \( F O L L O W(B) \) IV. If \( A \longrightarrow \alpha B A_{1} A_{2} \ldots A_{k} \) then add FIRST \( \left(A_{1}\right)-\{\varepsilon\} \) to FOLLOW (B) V. 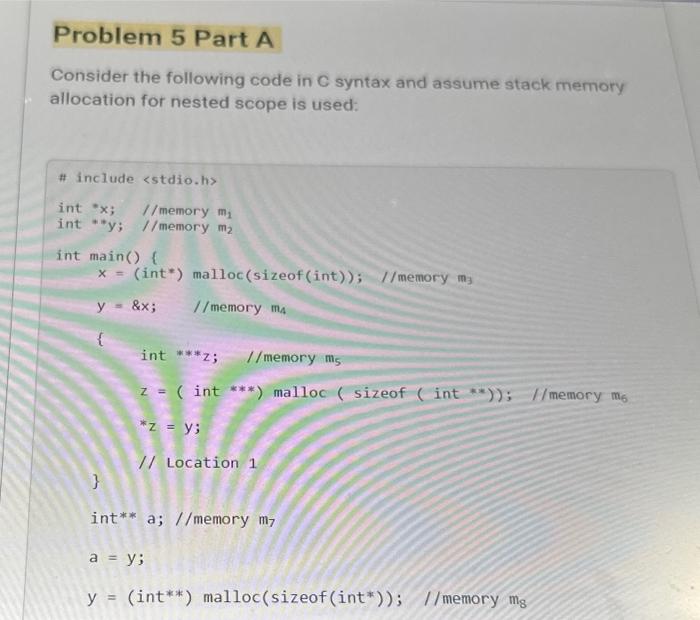If \( A \longrightarrow \alpha B A_{1} A_{2} A_{3} \ldots A_{i} A_{i+1} \ldots A_{k} \) and \( \varepsilon \in F I R S T\left(A_{1}\right) \) and \( \varepsilon \in F I R S T\left(A_{2}\right) \) and \( \ldots \) \( \varepsilon \in F I R S T\left(A_{i}\right) \) then add \( F I R S T\left(A_{i+1}\right)-\{\varepsilon\} \) to \( F O L L O W(B) \) Consider the following code in \( \mathrm{C} \) syntax and assume stack memory allocation for nested scope is used: int \( x ; \quad 1 / \) memory \( \mathrm{m}_{1} \) int **; \( y \); //memory \( m_{2} \) int main( ) \{ \( x=( \) int*) malloc(sizeof \( ( \) int \( )) ; \quad / / \) memory \( \mathrm{m}_{3} \) \( y=8 x ; \quad 1 / \) memory \( m_{4} \) \{ int \( * * * z ; \quad 1 / \) memory \( \mathrm{m}_{5} \) \( z=\left(\right. \) int \( \left.{ }^{* * *}\right) \) malloc \( \left(\right. \) sizeof \( \left(\right. \) int \( \left.\left.{ }^{* *}\right)\right) ; 1 / \) memory \( m_{6} \) \( * z=y \) 1/ Location 1 3 int** a; //memory \( \mathrm{m}_{7} \) \( a=y ; \) \( y=( \) int** \( ) \) malloc \( \left(\right. \) sizeof \( \left(\right. 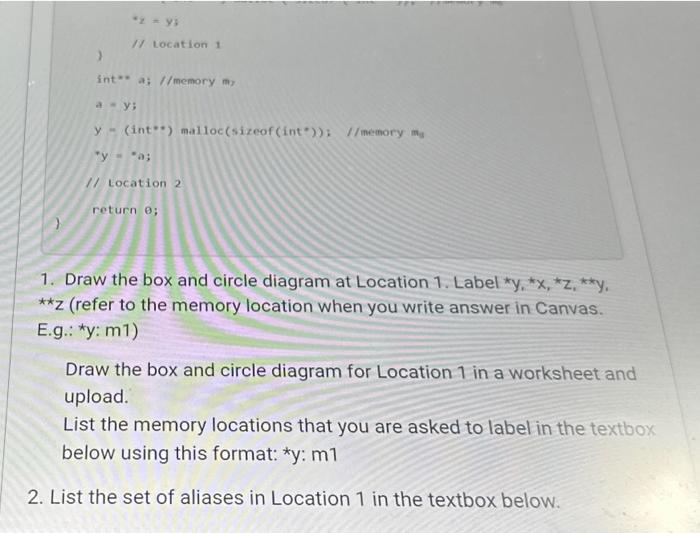\) int \( \left.\left.^{*}\right)\right) ; \quad / / \) memory mo 1. Draw the box and circle diagram at Location 1. Label \( * y \), \( * x, \star z, * \star y \), \( \star \star z \) (refer to the memory location when you write answer in Canvas. E.g.: \( \left.{ }^{\star} \mathrm{y}: \mathrm{m} 1\right) \) Draw the box and circle diagram for Location 1 in a worksheet and upload. List the memory locations that you are asked to label in the textbox: below using this format: * \( y \) : \( m 1 \) 2. List the set of aliases in Location 1 in the textbox below. 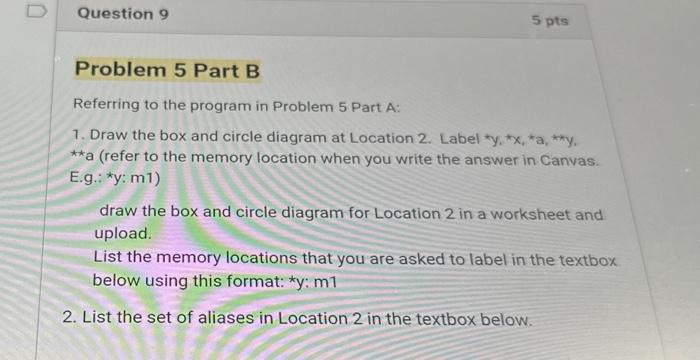Referring to the program in Problem 5 Part A: 1. Draw the box and circle diagram at Location 2. Label *y, * \( x \), *a, **y, \( \star \star \) a (refer to the memory location when you write the answer in Canvas. E.g..: \( \left.{ }^{*} \mathrm{y}: \mathrm{m} 1\right) \) draw the box and circle diagram for Location 2 in a worksheet and upload. List the memory locations that you are asked to label in the textbox below using this format: \( { }^{\star} \mathrm{y}: \mathrm{m} 1 \) 2. List the set of aliases in Location 2 in the textbox below.