(Solved): Find the normal vector N() to r()=Rcos(),sin(), the circle of radius R. Consider the ...

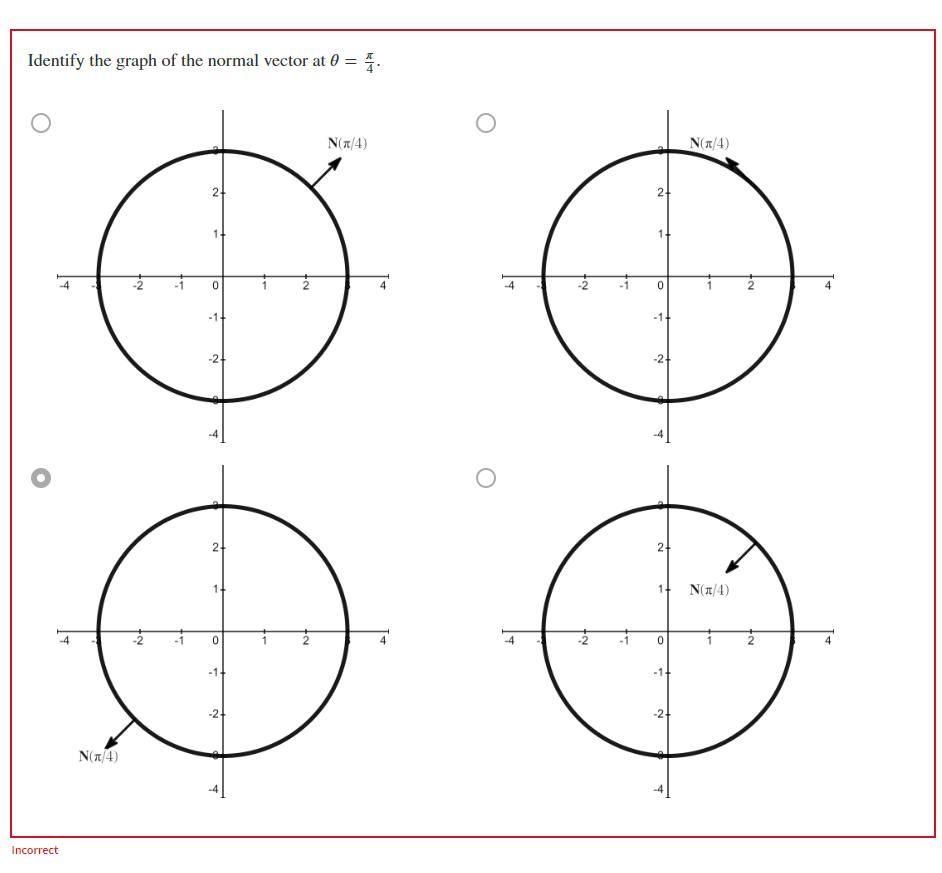
Find the normal vector $\mathbf{N}(\theta )$ to $\mathbf{r}(\theta )=R⟨\cos (\theta ),\sin (\theta )⟩$, the circle of radius $R$. Consider the following approach to find the direction $\mathbf{N}$ points. First find the unit tangent vector. $\begin{array}{rl}\mathbf{T}(\theta )& =\frac{{\mathbf{r}}^{\prime }(\theta )}{\Vert {\mathbf{r}}^{\prime }(\theta )\Vert }\\ \mathbf{T}(\theta )& =\frac{R⟨-\sin (\theta ),\cos (\theta )⟩}{|R|(1)}\\ \mathbf{T}(\theta )& =⟨-\sin (\theta ),\cos (\theta )⟩\end{array}$ Next, find the unit normal vector. $\begin{array}{l}\mathbf{N}(\theta )=\frac{{\mathbf{T}}^{\prime }(\theta )}{\Vert {\mathbf{T}}^{\prime }(\theta )\Vert }\\ \mathbf{N}(\theta )=⟨-\cos (\theta ),-\sin (\theta )⟩\end{array}$ Let $R=3$ and $\theta =\frac{\pi }{4}$ and obtain the graph of $\mathbf{N}(\theta )$ pointing outside the circle. Is this the correct graphical interpretation of the normal vector at the point $\theta =\frac{\pi }{4}$. If not, explain. This is a(n) since the normal vector Incorrect Identify the graph of the normal vector at $\theta =\frac{\pi }{4}$.