(Solved): Find the Maclaurin series for ()=ln(18^5) (1 point) Find the Maclaurin series ...

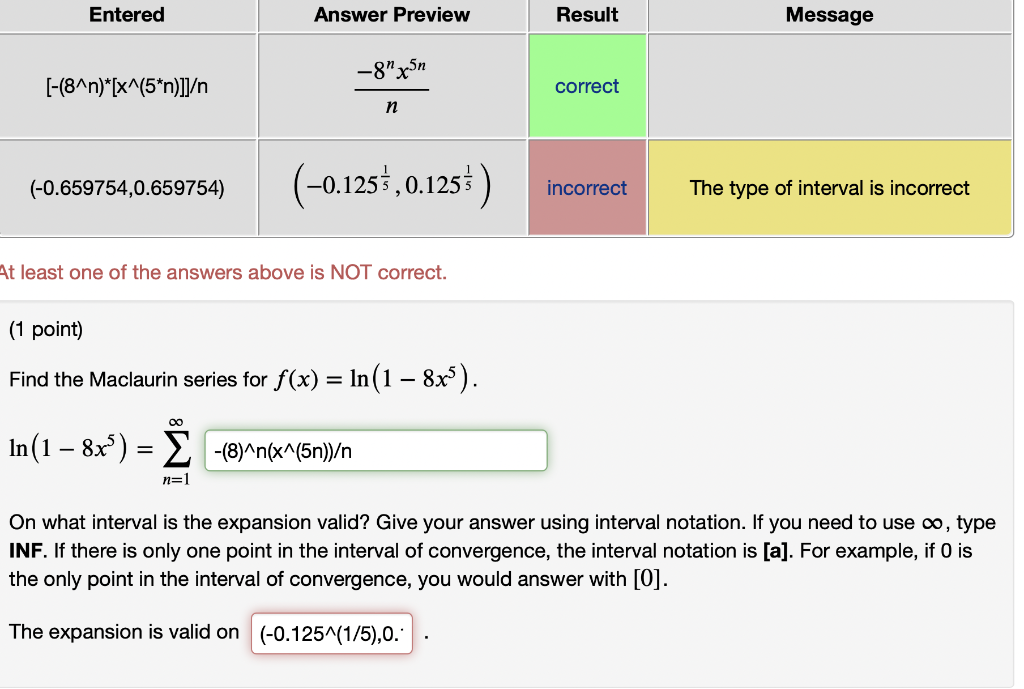
Find the Maclaurin series for ????(????)=ln(1?8????^5)

(1 point) Find the Maclaurin series for \( f(x)=\ln \left(1-8 x^{5}\right) \). \[ \ln \left(1-8 x^{5}\right)=\sum_{n=1}^{\infty} \] On what interval is the expansion valid? Give your answer using interval notation. If you need to use \( \infty \), type INF. If there is only one point in the interval of convergence, the interval notation is [a]. For example, if 0 is the only point in the interval of convergence, you would answer with [0]. The expansion is valid on