Home /
Expert Answers /
Advanced Physics /
figure-beside-shows-a-vertical-spring-mass-system-the-springs-are-identical-with-spring-c-pa906
(Solved): Figure beside shows a vertical spring mass system. The springs are identical with spring c ...

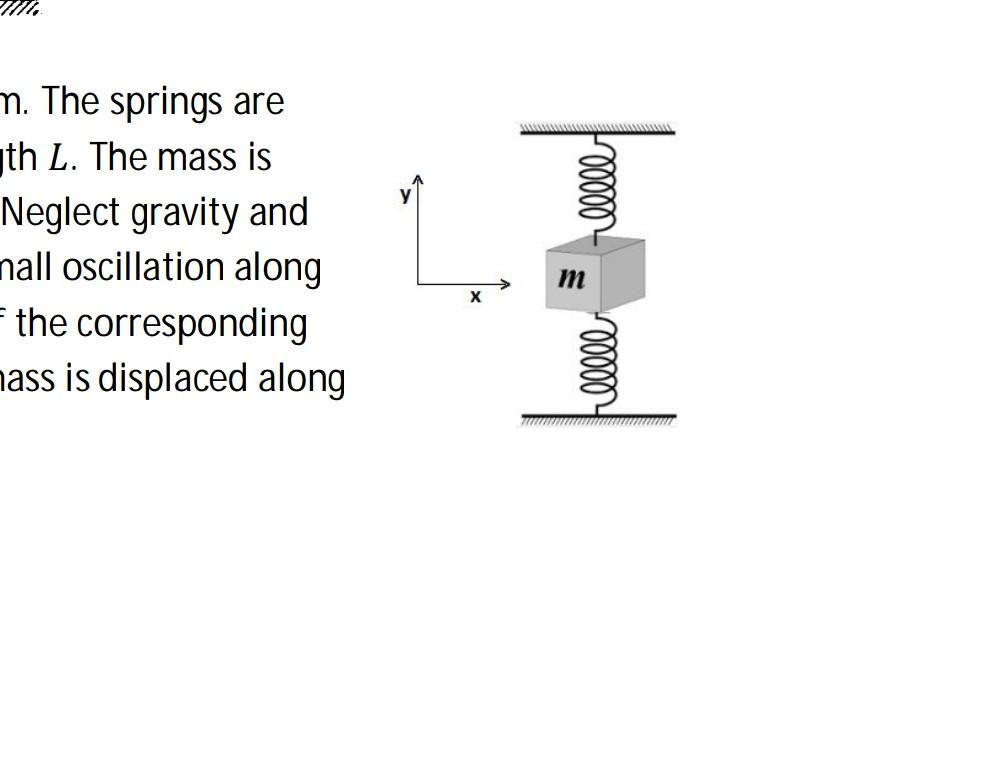
Figure beside shows a vertical spring mass system. The springs are
identical with spring constant ? and original length ?. The mass is
slightly displaced along the horizontal direction. Neglect gravity and
obtain the equation of motion of the mass for small oscillation along
the horizontal direction. Give a schematic plot of the corresponding
potential.What happens to the potential if the mass is displaced along
vertical direction?
please solve step by step
4. Figure beside shows a vertical spring mass system. The springs are identical with spring constant and original length . The mass is slightly displaced along the horizontal direction. Neglect gravity and obtain the equation of motion of the mass for small oscillation along the horizontal direction. Give a schematic plot of the corresponding potential. What happens to the potential if the mass is displaced alone vertical direction?
. The springs are th . The mass is Neglect gravity and nall oscillation along the corresponding lass is displaced along
Expert Answer
Here is a step-by-step solution to the problem:
First, we need to find the force on the mass due to the two springs. Since the springs are identical, the force on the mass due to each spring is the same. By Hooke's law, the force due to a spring is given by:
where F is the force, k is the spring constant, and x is the displacement from the equilibrium position.
In this case, the mass is displaced from the equilibrium position by a distance x in the horizontal direction, so the force on the mass due to each spring is:
F = -kx
2. To find the net force on the mass, we need to add up the forces due to the two springs. Since the springs are in series, the displacements are the same, so the net force on the mass is:
3. Using Newton's second law, we can relate the net force to the acceleration of the mass:
Substituting the net force from step 2, we get: