(Solved): Figure 1 shows a closed tank which is completely filled with water and connec ...

???????

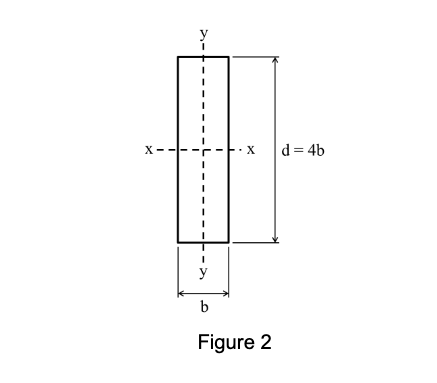
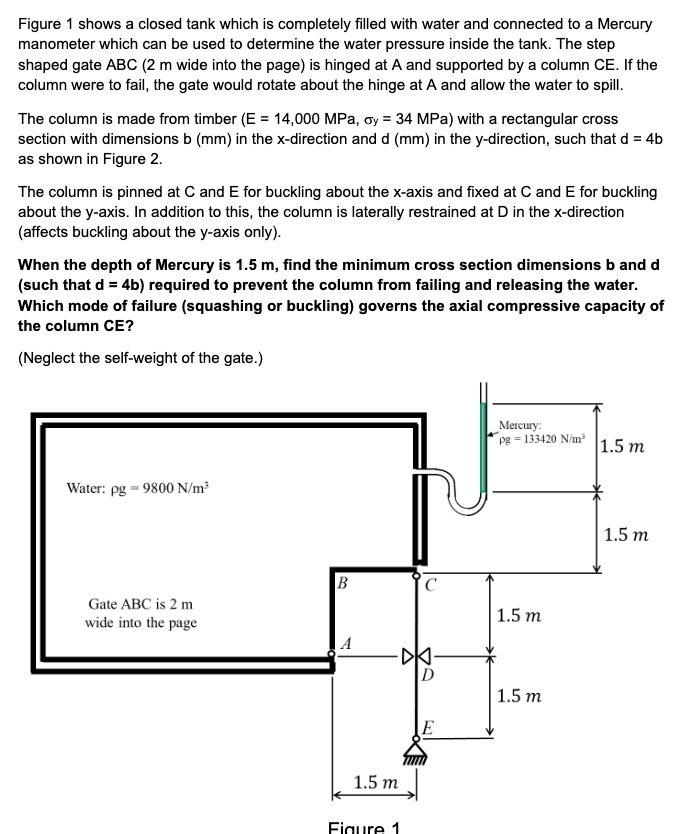
Figure 1 shows a closed tank which is completely filled with water and connected to a Mercury manometer which can be used to determine the water pressure inside the tank. The step shaped gate \( A B C \) ( \( 2 \mathrm{~m} \) wide into the page) is hinged at \( A \) and supported by a column \( C E \). If the column were to fail, the gate would rotate about the hinge at \( \mathrm{A} \) and allow the water to spill. The column is made from timber \( \left(\mathrm{E}=14,000 \mathrm{MPa}, \sigma_{\mathrm{y}}=34 \mathrm{MPa}\right) \) with a rectangular cross section with dimensions \( b(\mathrm{~mm}) \) in the \( x \)-direction and \( d(\mathrm{~mm}) \) in the \( y \)-direction, such that \( d=4 b \) as shown in Figure 2. The column is pinned at \( \mathrm{C} \) and \( \mathrm{E} \) for buckling about the \( \mathrm{x} \)-axis and fixed at \( \mathrm{C} \) and \( \mathrm{E} \) for buckling about the \( y \)-axis. In addition to this, the column is laterally restrained at \( D \) in the \( x \)-direction (affects buckling about the \( y \)-axis only). When the depth of Mercury is \( 1.5 \mathrm{~m} \), find the minimum cross section dimensions \( b \) and \( d \) (such that \( d=4 b \) ) required to prevent the column from failing and releasing the water. Which mode of failure (squashing or buckling) governs the axial compressive capacity of the column CE? (Neglect the self-weight of the gate.) Figure 2