(Solved): Fig. 1 By applying the KVL rule, we can obtain the circuit's first order differential equation ...

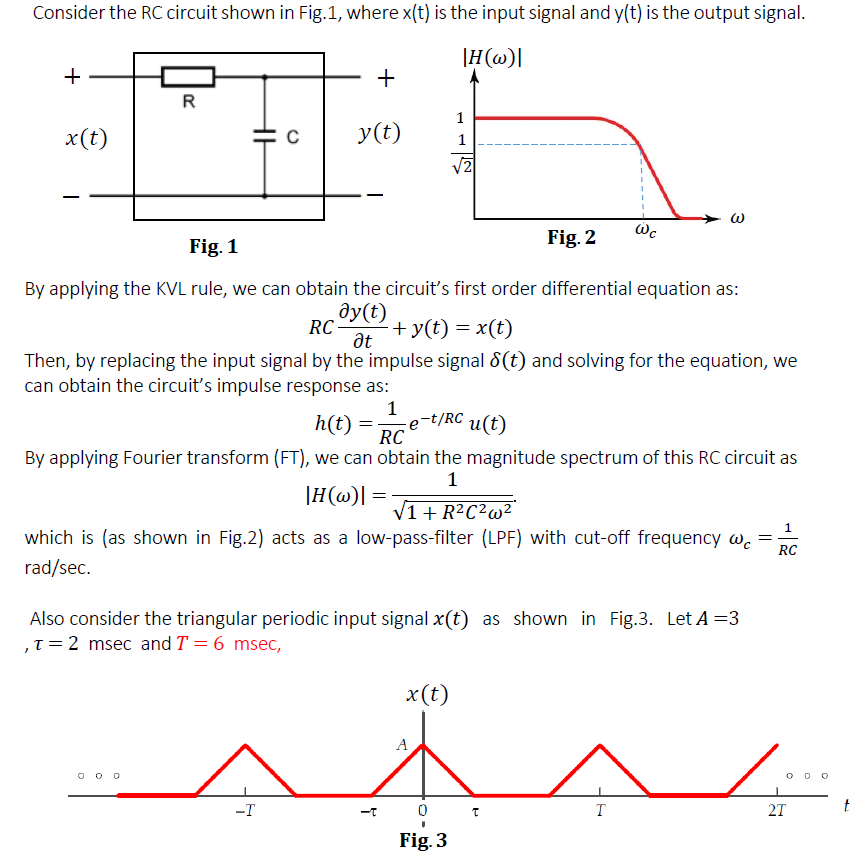
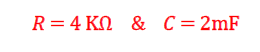
Fig. 1 By applying the KVL rule, we can obtain the circuit's first order differential equation as: $RC\frac{\partial y(t)}{\partial t}+y(t)=x(t)$ Then, by replacing the input signal by the impulse signal $\delta (t)$ and solving for the equation, we can obtain the circuit's impulse response as: $h(t)=\frac{1}{RC}{e}^{-t/RC}u(t)$ By applying Fourier transform (FT), we can obtain the magnitude spectrum of this RC circuit as $|H(\omega )|=\frac{1}{\sqrt{1+R^2{C}^2{\omega }^2}}$ which is (as shown in Fig.2) acts as a low-pass-filter (LPF) with cut-off frequency ${\omega }_c=\frac{1}{RC}$ $\mathrm{rad}/\sec$. Also consider the triangular periodic input signal $x(t)$ as shown in Fig.3. Let $A=3$ ,$\tau =2\mathrm{msec}$ and $T=6\mathrm{msec}$ $R=4\mathrm{K}\Omega \&C=2\mathrm{mF}$ The aim of this part is to use a numerical analysis tool (MATLAB/Octave) to help students to obtain the frequency harmonics of a triangular periodic signal by applying Fourier series (FS), and to design a low-pass-filter to remove the high frequency components from the signal. For this purpose, consider the triangular periodic signal $x(t)$ shown in Fig. 3 . 1- Determine the fundamental frequency ${\omega }_o$ of the periodic signal $x(t)$, and write a MATALB code to generate and plot it in the time domain for $t\in \left[-\frac{T}{2},\frac{T}{2}\right]$. 2- Write a MATLAB code to compute its Fourier series coefficients $a_k$ and to plot its magnitude spectrum $\left|a_k\right|$ versus $k\in [-100,100]$. 3- Design the RC circuit shown in Fig. 1 (i.e., find the values of R and C)such that the cutoff frequency value ${\omega }_c=4{\omega }_o$; specifically: - Determine the required values of $\mathrm{R}$ and $\mathrm{C}$. - Write a MATLAB code to plot the magnitude spectrum of the filter $|H(\omega )|$. - Write a MATLAB code to plot the filtered output signal in the frequency domain. - Write a MATLAB code to compute and plot the filtered output signal in the time domain. - Compare it with the original input signal $x(t)$ and discuss the differences with reasonable justifications.