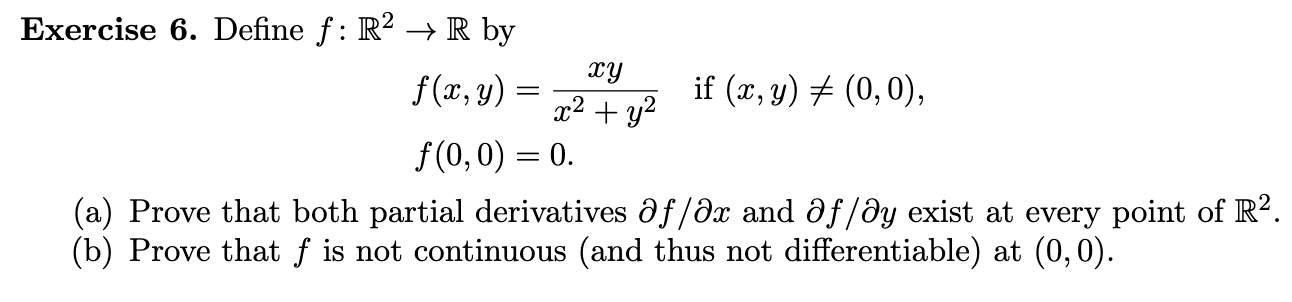(Solved): Exercise 6. Define \( f: \mathbb{R}^{2} \rightarrow \mathbb{R} \) by \[ \begin{aligned} f(x, y) & ...

Exercise 6. Define \( f: \mathbb{R}^{2} \rightarrow \mathbb{R} \) by \[ \begin{aligned} f(x, y) & =\frac{x y}{x^{2}+y^{2}} \quad \text { if }(x, y) \neq(0,0), \\ f(0,0) & =0 . \end{aligned} \] (a) Prove that both partial derivatives \( \partial f / \partial x \) and \( \partial f / \partial y \) exist at every point of \( \mathbb{R}^{2} \). (b) Prove that \( f \) is not continuous (and thus not differentiable) at \( (0,0) \).