Home /
Expert Answers /
Civil Engineering /
equation-of-the-parabola-in-figure-1-is-y-51-400x2-determine-the-moment-of-inertia-of-th-pa645
(Solved): Equation of the parabola in (Figure -1) is y=51(400x2). Determine the moment of inertia of th ...
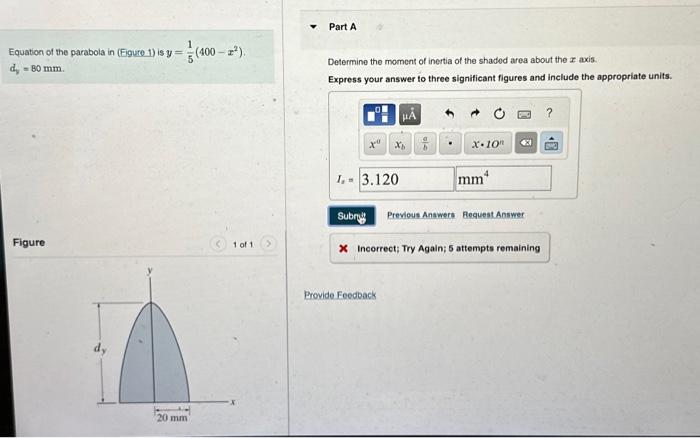
Equation of the parabola in (Figure -1 is . Determine the moment of inertia of the shadod area about the axis. . Express your answer to three significant figures and include the appropriate units.
Expert Answer
To find the moment of inertia of the shaded area about the x-axis, we need to first find the equation of the parabolic curve in terms of y, since the differential element dA will be in terms of dy. We can rewrite the equation of the parabola as:x = ±?(400 - 5y)Since the area is symmetric about the y-axis, we only need to consider the positive half of the parabola. Therefore, the differential element dA can be expressed as:dA = 2y dxSubstituting x = ?(400 - 5y), we get:dA = 2y d(?(400 - 5y)) = 2y / (2?(400 - 5y)) (-5/2) dy